Maximum Bipartite Graph

This is the most famous question in graph theory, where you have to find the maximum number of dots in the first set, to be connected with dots in the second set, with a condition that no two nodes can be connected from first to second and vice-versa.

Let me first give a brief intro about the problem statement.
There are M number of job applicants, applying for N number of jobs. Each job opening can only accept one applicant and a job applicant can be appointed for only one job.

The Bruteforce Method is to give the job to the applicant, that is on their first priority, if there occurs any conflict, then move on to its second-most priority, and so on.
But from this approach, we won't be able to get the maximum number of jobs to be given to the applicants.

Optimised Approach

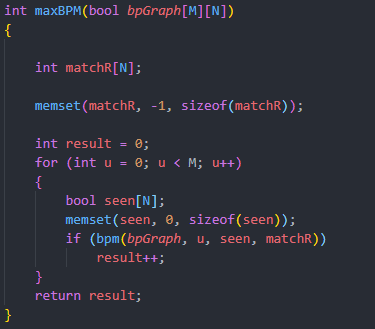
We are given a 2-D matrix, in which, if the job applicant has applied for a particular job, then it equals to 1 otherwise 0.
First of all, we will make matchR[] array of size N(number of total jobs available) and initialize it with -1 as follows:

Now, loop through the job applicants, and initialize another boolean array with false, named seen, it will keep track if the same job is not given to two applicants.

Now call the function bpm

It will check the first priority of the first applicant, it will normally assign that job to him. Then we will send the second job applicant, it will check it's the first priority if his first priority is the same as that given to the previous applicant, then we will recursively call the function again and check if
the second priority of the previous one is available,
if is available {
then it would be assigned to him, and our present applicant can get his first priority job.}
otherwise {
check for the next priority job of the same previous job applicant.
}
Now consider, if the previous applicant doesn't have second priority, then we don't give the job to the present job applicant and will return false, and move on to next one.

In this way, we can get the maximum number of jobs that can be given to the applicants.
That's all.
Keep reading :)
Keep coding :)