When it comes to Data Structures, few are preceded by as much of a reputation as the Binary Search Tree.
While it may not come up quite so often on the job, understanding how a BST functions and how it's built are important fundamentals to understand for technical interviews, and for understanding some deeper aspects of recursion.
What is a Binary Search Tree?
A Binary Search Tree is a variation of a regular Binary Tree, a data structure in which each node has at most two children. What differentiates a Binary Search Tree from a regular Binary Tree is that the value of each left node is less than its parent, while the value of each right node is greater than its parent.
Here's a visualized example:
10
/ \
8 12
/ \ / \
4 9 11 15
As you can see, this is a valid Binary Search Tree, because it fulfills the rule of lesser and greater values in the proper positions.
How do we build one?
I'm glad you asked! Let's go through the steps together to build one out in modern JavaScript.
We're going to be building our BST using ES6 Class syntax, and it can actually all be done within one class!
Let's declare it first, and build out our constructor at the same time:
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
}
What we've put into the constructor is everything we need for the actual data of each node in the tree. The node has its own data, passed in as an argument, and has a left node and a right node, both of which are set to null by default. Easy!
Now, let's build out a class method to insert a new node into the tree. Remember, we need to make sure that this method compares the given data against both the left and right values of the current node, as well as properly works its way down the existing tree from the node.
We can do it in two parts, like so:
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
insert(data) {
if (data < this.data && this.left) {
this.left.insert(data);
} else if (data < this.data) {
this.left = new Node(data);
}
if (data > this.data && this.right) {
this.right.insert(data);
} else if (data > this.data) {
this.right = new Node(data);
}
}
}
Essentially this is doing the same thing on both the right and the left.
We're checking to see if our passed in data is less than or greater than the current node's data, and then seeing if a left or right node already exists for the current node.
If not, then we insert this data as a new node in the proper position. If there is a node there already, then we call the insert method again on the left or right node, depending on which direction we're moving in. This repeats the process below, in that child node.
In terms of building a Binary Search Tree, we're basically done now. Yay!
Let's go one step further though and implement one more method to see if a BST contains a certain value:
class Node {
constructor(data) {
this.data = data;
this.left = null;
this.right = null;
}
insert(data) {
if (data < this.data && this.left) {
this.left.insert(data);
} else if (data < this.data) {
this.left = new Node(data);
}
if (data > this.data && this.right) {
this.right.insert(data);
} else if (data > this.data) {
this.right = new Node(data);
}
}
contains(data) {
if (this.data === data) {
return this;
}
if (data < this.data && this.left) {
return this.left.contains(data);
} else if (data > this.data && this.right) {
return this.right.contains(data);
} else {
return null;
}
}
}
We're essentially doing the same thing here that we did above with the insert method.
We compare the given data against the data of the current node, seeing if its less than or greater than, and if a left or right node exists then we call the same contains method on it to check its data and children.
If the value is less than or greater than the current data and no left or right child node exists respectively, then we know the value doesn't exist in the tree and return null.
The key aspect of this method is our "base case", or the first three lines in the function. This checks to see if the current node's data is equal to the value we're searching for, and if so, we've found a match! We can return that node, or any other value we choose to confirm a hit.
And there you have it! We've officially built out a simple, functional Binary Search Tree in JavaScript. I'll explore some further functionalities of a BST in later blog posts that go a bit deeper on other interview questions you may come across involving them.
If you've read this far, thanks so much for taking the time. I hope it's been helpful! :)
Top comments (8)
I didn't touch a binary since 2018 ( when I studied them the first time in Java). Now that I am studying JS I want to challenge myself to replicate all my old searching methods in JS too. Ty for inspiration for this new exercise 😁👍!
Just a minor note: you've overlooked the case where the value of the node you're trying to insert is equal to the current node, not strictly greater than or less than the node's value. Either the left or right subtree can be arbitrarily chosen for this, as long as you're consistent.
Thank you very much for the heads up, Aleksandr! I hadn't considered that case, although it seems quite obvious now that you mention it. I'll keep that in mind moving forward. 👍
Nice use of recursion, I'll give it a try with typescript soon
hi Sean
thanks for your code , looks nice look this is a silly question ,
but how i can initite and create new object with this class?
i did this :::
let nodos = new Node();
nodos.insert(1);
nodos.insert(9);
then i type:
console.log(nodos.contains(9));
give me null.
please let me know i am learning algorithms with java and trying to learn deep javascript .
thanks
hi Sean
thanks for your code , looks nice look this is a dumb question , but how i can initite and create new object with this class?
please let me know i am learning algorithms with java and trying to learn deep javascript .
thanks
hi @seanwelshbrown nice implementation in JS. But this is failing when the values are in incremental order itself.
Lets take example of 1,2,3,4
then the output is this - [It have only right nodes]
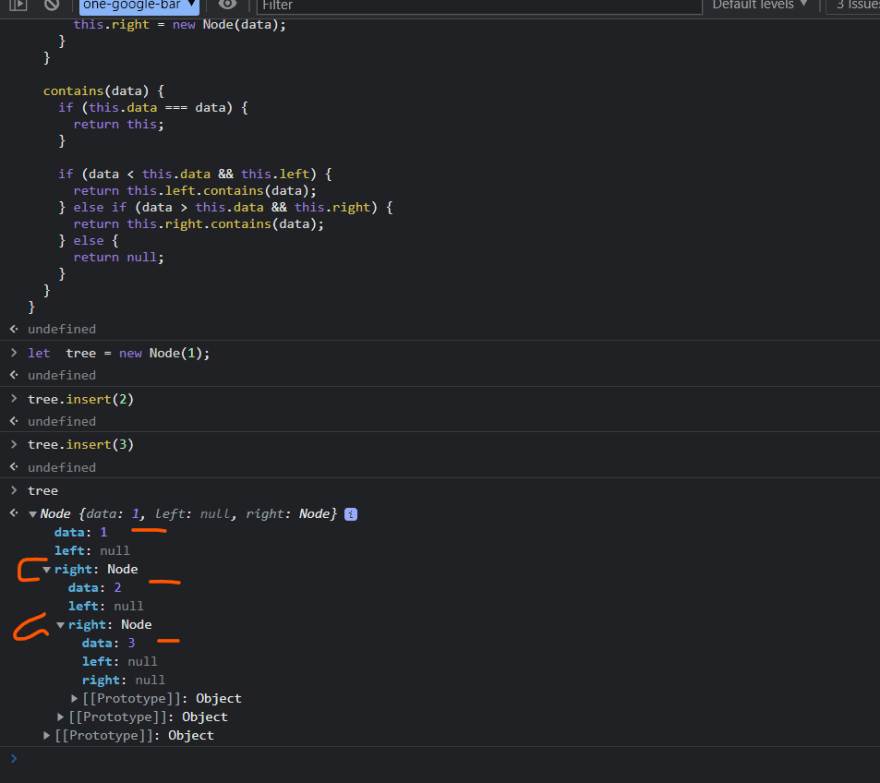
Update: I got it, it will become unbalanced binary tree when input is 1,2,3,4
Very helpful and simple solution, thank you