What is Big O Notation?
In Computer Science, Big O Notation is used to describe the performance of an algorithm. In other words, how well will this algorithm scale as the input grows larger? With Big O Notation, we are always taking into consideration the worst case because that is how we will see how efficient our algorithm is.
I do want to preface this by saying, we are not concerned with how fast your program runs. That is dependent on various different things like:
- How old is your computer?
- How much RAM does it have?
- How many CPU's does it have?
I think you get the point.
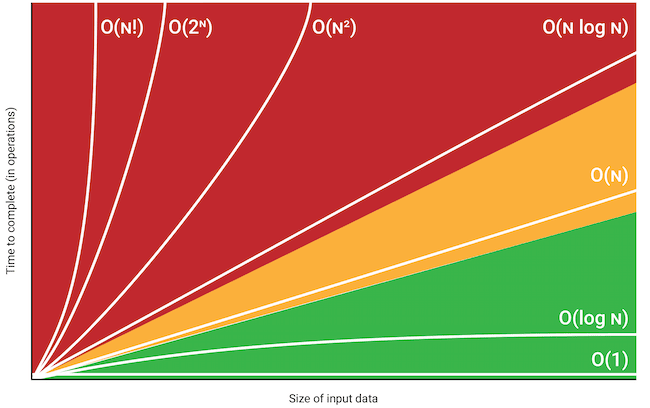
Here is a great visualization of Big O Notation.
O(1)
O(1) means the algorithm runs in constant time. No matter how large the input/data size, the run time complexity of this algorithm is in constant time. It never changes.
The cost of this operation is constant. It does not matter if the data set is 10 or 1,000,000. You are only accessing the first index of the array.
O(N)
O(n) means the algorithms runs in linear time. As the data/input size grows, the run time complexity of this algorithm increases.
The cost of this operation grows linearly. This is because we are looping over the array. This array be be 10 or 1,000,000. This means it would also print 10 or 1,000,000 times.
O(N^2)
O(N^2) means our algorithm runs in quadratic time. As our data/input size grows, our algorithm gets slower and slower.
The cost of this operations grows in quadratic time. This is because we are doing one loop throw an array, and within that loop, we are doing another loop. So, you can imagine that if we had 1,000,000 values in our array, our algorithm would not be very efficient.
O(Log N)
O(Log N) means our algorithm runs in logarithmic time. As our data/input size gets larger, the more efficient our algorithm is.
Examples include:
- Binary Search
- Certain Divide and Conquer Algorithms
- Calculating Fibonacci Numbers





Top comments (0)