Thinking about all of the abstractions that surround us in the world of technology can sometimes be overwhelming. This is particularly true when you’re trying to wrap your head around a new paradigm or unpack the layers of one or many concepts that you’re struggling to understand.
In the context of learning computer science, there are simply too many abstractions to know, see, or recognize them all — not to mention being able to comprehend all of them!
Abstractions are powerful things when you can see beyond them, and being able to uunderstand how something is abstracted away and why can make you a better programmer. However, by the same token, every abstraction was created for a reason: so that none of us would have to worry about them on a day-to-day basis! We’re not meant to think about abstractions all the time, and for the most part, very few of us actually do. Here’s the thing though — some abstractions are more equal than others. The ones that most engineers are probably concerned with are the ones that involve how they communicate with their computer, and the ways in which their computer actually understands them. Even if we none of us ever have to write a bubble sort algorithm, if we write code, then we have to communicate with our machines.
Well, it’s finally time for us to get to the bottom of these mysteries, and understand the abstractions which power our workflows as programmers.
Parsing for the meaning of parsing
The tree data structure is one that keeps coming up again and again in our computer science adventures. We’ve seen them used to store data of all types, we’ve seen ones that are self-balancing, while others have been optimized for space and handling storage. We’ve even looked at how to manipulate trees by rotating and recoloring them to ensure that they fit a set of rules.
But despite all of these different forms of data structure flora, there is one particular iteration of the tree data structure that we have yet to discover. Even if we knew nothing about computer science, how to balance a tree, or what a tree data structure even works, all programmers interact with one type of tree structure on a daily basis, by virtue of the simple fact that every developer who writes code needs to make sure that their code is understood by their machines.
This data structure is called the parse tree, and it is (one of) the underlying abstractions that allows the code that we write as programmers to become “readable” by our computers.
At its very core, a parse tree is an illustrated, pictorial version of the grammatical structure of a sentence. Parse trees are actually rooted in the field of linguistics, but they’re also used in pedagogy, which is the study of teaching. Parse trees are often used to teach students how to identify the parts of a sentence, and are a common way of introducing grammatical concepts. It’s likely that we’ve each interacted with them from the persepctive of sentence diagramming, which some of us might have learned in elementary school.
A parse tree is a really just a “diagrammed” form of a sentence; that sentence could be written in any language, which means that it could adhere to any set of grammatical rules.
Sentence diagramming involves breaking up a single sentence into its smallest, most distinct parts. If we think about parse trees from the persepctive of diagramming sentences we’ll begin to quickly realize that, depending on the grammar and language of a sentence, a parse tree could really be constructed in a multitude of different ways!
But what exactly is a the computer version of a “sentence”? And how do we go about diagramming it, exactly?
Well, it helps to start with an example of something that we’re already comfortable with, so let’s refresh our memories by diagramming a normal, English sentence.

In the illustration shown here, we have a simple sentence: "Vaidehi ate the pie". Since we know that a parse tree is just a diagrammed sentence, we can build a parse tree out of this example sentence. Remember that effectively all we’re trying to do is to determine the different parts of this sentence and break it up into its smallest, most distinct parts.
We can start by breaking up the sentence into two parts: a noun , "Vaidehi", and a verb phrase , "ate the pie". Since a noun cannot be broken down any further, we’ll leave the word "Vaidehi", as it is. Another way to think about it is the fact that, since we can’t break down a noun any further, there will be no child nodes coming from this word.
But what about the verb phrase, "ate the pie"? Well, that phrase isn’t broken down into its simplest form yet, is it? We can dissect it down even further. For one thing, the word "ate" is a verb, while "the pie" is more of a noun — in fact, it’s a noun phrase to be completely specific. If we split up "ate the pie", we can divide it into a verb and a noun phrase. Since a verb cannot be diagrammed with any additional detail, the word "ate" will become a leaf node in our parse tree.
Alright, so all that’s left now is the noun phrase, "the pie". We can split this phrase up into two distinct pieces: a noun, "pie", and its determiner , which is known as any modifying word of a noun. In this case, the determiner is the word "the".
Once we divide up our noun phrase, we’re done splitting up our sentence! In other words, we’re done diagramming our parse tree. When we look at our parse tree, we’ll notice that our sentence still reads the same way, and we haven’t actually modified it at all. We just took the sentence we were given, and use the rules of English grammar to split it up into its smallest, most distinct parts.
In the case of the English language, the smallest “part” of every sentence is a word; words can be combined into phrases, like noun phrases or verb phrases, which can, in turn, be joined with other phrases to create a sentence epression.

However, this is just one example of how one specific sentence, in one specific language, with its own set of grammatical rules would be diagrammed into a parse tree. This same sentence would look very different in a different language, especially if it had to follow its own set of grammatical rules.
Ultimately, the grammar and syntax of a language — including the way the sentences of that language are structured — become the rules that dictate how that language is defined, how we write in it, and how those of us who speak the language will end up understanding and interpreting it.
Interestingly, we knew how to diagram the simple sentence, "Vaidehi ate the pie." because we were already familiar with the grammar of the English language. Imagine if our sentence was missing a noun or a verb altogether? What would happen? Well, we’d likely read the sentence the first time around and quickly realize that it wasn’t even a sentence at all! Rather, we’d read it, and almost immediately see that we were dealing with a sentence fragment , or an incomplete piece of a sentence.
However, the only reason that we’d be able to recognize a sentence fragment is if we knew the rules of the English language — namely, that (nearly) every sentence needs a noun and a verb to be considered valid. The grammar of a language is how we can check to see if a sentence is valid in a language; that process of “checking” for validity is referred to as parsing a sentence.
The process of parsing a sentence to understand it when we read it for the first time involves the same mental steps as diagramming a sentence, and diagramming a sentence involves the same steps as building a parse tree. When we read a sentence for the very first time, we’re doing the work of mentally deconstructing and parsing it.
As it turns out, computers do the exact same thing with the code that we write!
Parsing expressions like it’s our job
Okay, so we now know how to diagram and parse an English language sentence. But how does that apply to code? And what even is a “sentence” in our code?
Well, we can think of a parse tree as an illustrated “picture” of how our code looks. If we imagine our code, our program, or even just the simplest of scripts in the form of a sentence, we’d probably realize pretty quickly that all of the code that we write could really just be simplified into sets of expressions.
This makes a lot more sense with an example, so let’s look at a super simple calculator program. Using a single expression, we can use the grammatical “rules” of mathematics to create a parse tree from that expression. We’ll need to find the simplest, most distinct units of our expression, which means that we’ll need to break up our expression into smaller segments, as illustrated below.
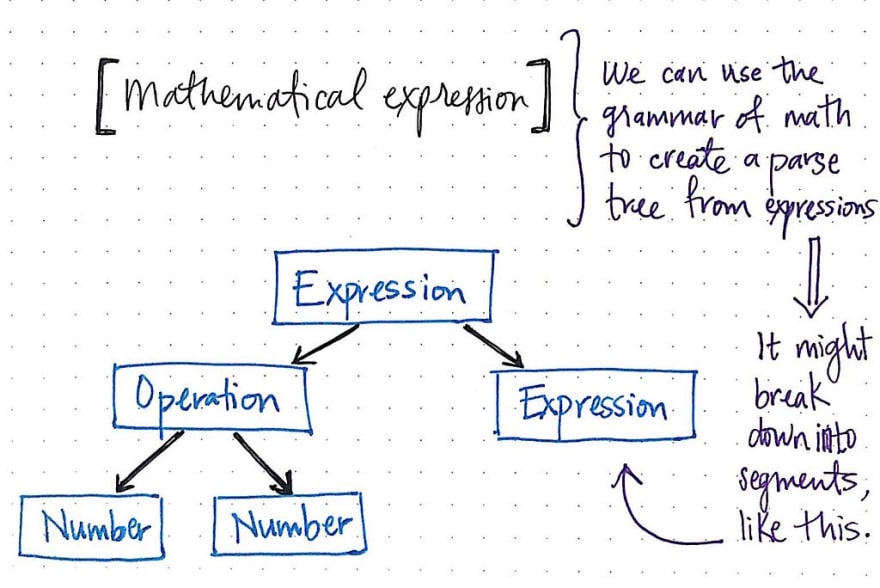
We’ll notice that a single mathematical expression has its own grammar rules to follow; even a simple expression (like two numbers being multiplied together and then added to another number) could be split up into even simpler expressions within themselves.
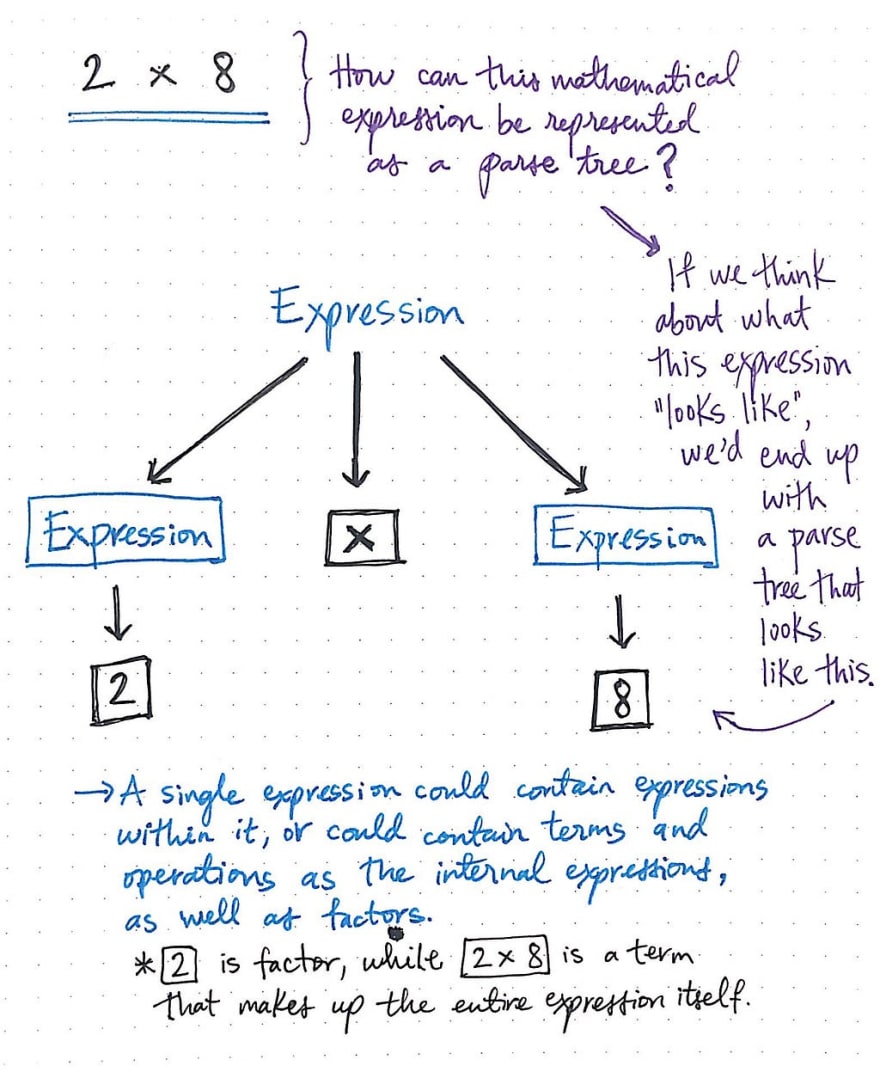
But let’s work with a simple calculation to start. How could we create a parse tree using mathematical grammar for an expression such as 2 x 8?
If we think about what this expression really looks like, we can see that there are three distinct pieces here: an expression on the left, an expression on the right, and an operation that multiplies the two of them together.
The image shown here diagrams out the expression 2 x 8 as a parse tree. We’ll see that the operator, x, is one piece of the expression that cannot be simplified any further, so it doesn’t have any child nodes.
The expression on the left and on the right could be simplified into its specific terms, namely 2 and 8. Much like the English sentence example we looked at earlier, a single mathematical expression could contain internal expressions within it, as well as individual terms, like the phrase 2 x 8, or factors, like the number 2 as an individual expression itself.
But what happens after we create this parse tree? We’ll notice that the hierarchy of child nodes here is a little less obvious than in our sentence example from before. both 2 and 8 are at the same level, so how could we interpret this?
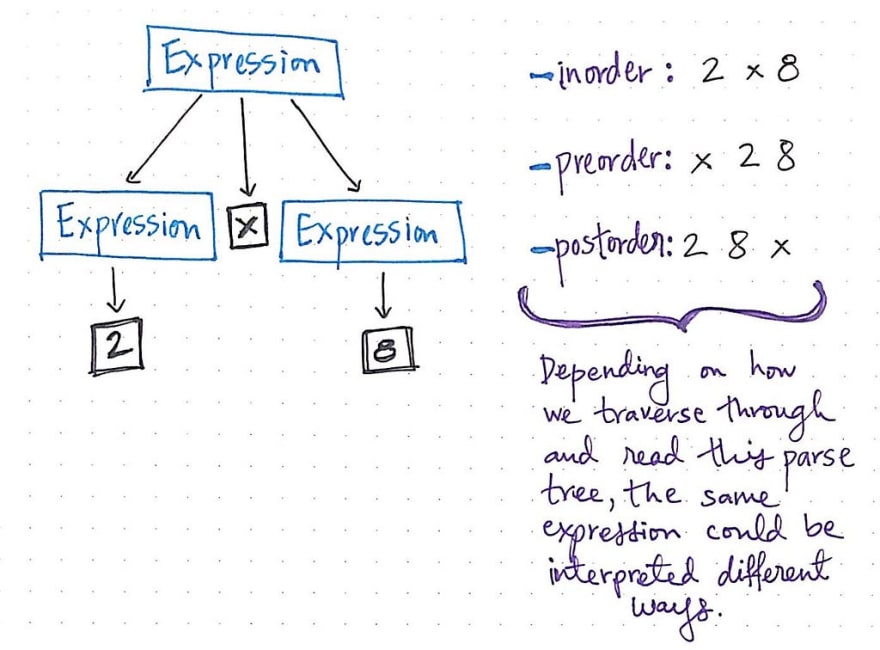
Well, we already know that there are various different ways to depth-first traverse through a tree. Depending on how we traverse through this tree, this single mathematical expression, 2 x 8 could be interpreted and read in many ways. For example, if we traversed through this tree using inorder traversal, we’d read the left tree, the root level, and then the right tree, resulting in 2 -> x -> 8.
But if we chose to walk through this tree using preorder traversal, we’d read the value at the root level first, followed by the left subtree and then the right subtree, which would give us x -> 2 -> 8. And if we used postorder traversal, we’d read the left subtree, the right subtree, and then finally read the root level, which would result in 2 -> 8 -> x.
Parse trees show us what our expressions look like, revealing the concrete syntax of our expressions, which often means that a single parse tree could express a “sentence” in various different ways. For this reason, parse trees are also often referred to as Concrete Syntax Trees , or CSTs for short. When these trees are interpreted, or “read” by our machines, there need to be strict rules as to how these trees are parsed, so that we end up with the correct expression, with all the terms in the correct order and in the right place!
But most expressions that we deal with are more complex than just 2 x 8. Even for a calculator program, we will probably need to do more complicated computations. For example, what happens if we wanted to solve for an expression like 5 + 1 x 12? What would our parse tree look like?
Well, as it turns out, the trouble with parse trees is that sometimes you can end up with more than one.

More specifically, there can be more than a single outcome for one expression that is being parsed. If we assume that parse trees are read from the lowest-level first, we can start to see how the heirarchy of the leaf nodes can cause the same expression to be interpreted in two totally different ways, yielding two totally different values as a result.
For example, in the illustration above, there are two possible parse trees for the expression 5 + 1 x 12. As we can see in the left parse tree, the heirarchy of the nodes is such that the expression 1 x 12 will be evaluated first, and then the addition will continue: 5 + (1 x 12). On the other hand, the right parse tree is very different; the heirarchy of the nodes forces the addition to happen first (5 + 1), and then moves up the tree to continue with multiplication: (5 + 1) x 12.
Ambiguous grammar in a language is exactly what causes this kind of situation: when its unclear how a syntax tree should be constructed, it’s possible for it to be built in (at least) more than one way.
Here’s the rub, though: ambiguous grammar is problematic for a compiler!

Based on the rules of mathematics that most of us learned in school, we know inherently that multiplication should always be done before addition. In other words, only the left parse tree in the above example is actually correct based on the grammar of math. Remember: grammar is what defines the syntax and the rules of any language, whether its an English sentence or a mathematical expression.
But how on earth would the compiler know these rules inherently? Well, there’s just no way that it ever could! A compiler would have no idea which way to read the code that we write if we don’t give it grammatical rules to follow. If a compiler saw that we wrote a mathematical expression, for example, that could result in two different parse trees, it wouldn’t know which of the two parse trees to choose, and thus, it wouldn’t know how to even read or interpret our code.
Ambiguous grammar is generally avoided in most programming languages for this very reason. In fact, most parsers and programming languages will intentionally deal with problems of ambiguity from the start. A programming language will usually have grammar that enforces precedence, which will force some operations or symbols to have a higher weight/value than others. An example of this is ensuring that, whenever a parse tree is constructed, multiplication is given a higher precedence than addition, so that only one parse tree can ever be constructed.
Another way to combat problems of ambiguity is by enforcing the way that grammar is interpreted. For example, in mathematics, if we had an expression like 1 + 2 + 3 + 4, we know inherently that we should begin adding from the left and work our way to the right. If we wanted our compiler to understand how to do this with our own code, we’d need to enforce left associativity, which would constrict our compiler so that when it parsed our code, it would create a parse tree that puts the factor of 4 lower down in the parse tree hierarchy than the factor 1.
These two examples often referred to as disambiguating rules in compiler design, as they create specific syntactical rules ensure that we never end up with ambiguous grammar that our compiler will be very confused by.
A token of my affection (for my parser)
If ambiguity is the root of all parse tree evil, then clarity is clearly the preferred mode of operation. Sure, we can add disambiguating rules to avoid ambiguous situations that’ll cause our poor little computer to be stumped when it reads our code, but we actually do a whole lot more than that, too. Or rather, it is the programming languages that we use that do the real heavy lifting!
Let me explain. We can think of it this way: one of the ways that we can add clarity to a mathematical expression is through parenthesis. In fact, that’s what most of us probably would do for the expression we were dealing with earlier: 5 + 1 x 12. We probably would have read that expression and, recalling the order of operations we learned in school, we would have rewritten it in our heads as: 5 + (1 x 12). The parenthesis () helped us gain clarity about the expression itself, and the two expressions that are inherently within it. Those two symbols are recognizable to us, and if we were putting them in our parse tree, they wouldn’t have any children nodes because they can’t be broken down any further.
These are what we refer to as terminals , which are also commonly known as tokens. They are crucial to all programming languages, because they help us understand how parts of an expression relate to one another, and the syntactic relationships between individual elements. Some common tokens in programming include the operation signs (+, -, x, /), parenthesis (()), and reserved conditional words (if, then, else, end). Some tokens are used to help clarify expressions because they can specify how different elements relate to one another.

So what are all the other things in our parse tree? We clearly have more than just if's and + signs in our code! Well, we also usually have to deal with sets of non-terminals , which are expressions, terms, and factors that can potentially be broken down further. These are the phrases/ideas that contain other expressions within them, such as the expression (8 + 1) / 3.
Both terminals and non-terminals have a specific relationship to where they appear in a parse tree. As their name might suggest, a terminal symbol will always end up as the leaves of a parse tree; this means that not only are operators, parenthesis, and reserved conditionals “terminals”, but so are all the factor values that represent the string, number, or concept that is at every leaf node. Anything that is broken down into its smallest possible piece is effectively always going to be a “terminal”.
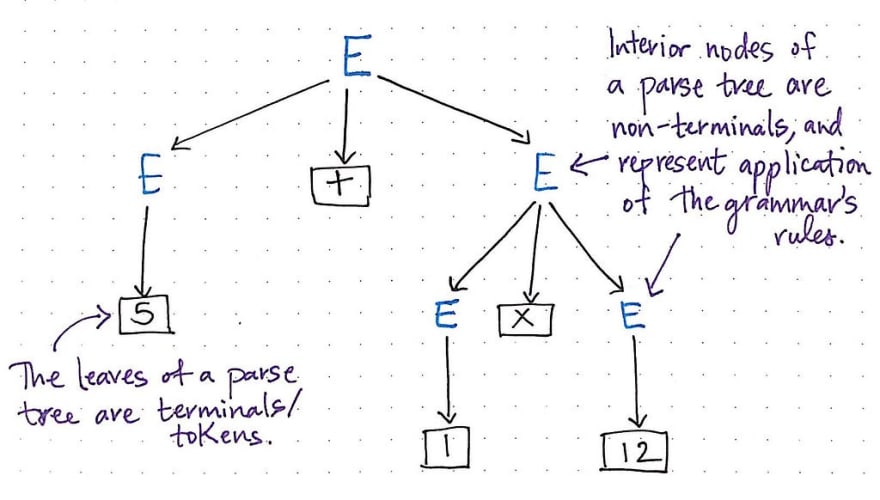
On the flip side, the interior nodes of a parse tree — the non-leaf nodes that are parent nodes — are the non-terminal symbols, and they’re the ones that represent the applicaiton of the programming language’s grammar rules.
A parse tree becomes a lot easier to understand, visualize, and identify once we can wrap our heads around the fact that it is nothing more than a representation of our program, and all of the symbols, concepts, and expressions within it.
But what is the value of a parse tree, anyways? We don’t think about it as programmers, but it must exist for a reason, right?

Well, as it turns out, the thing that cares about the parse tree the most is the parser , which is a part of a complier that handles the process of parsing all of the code that we write.
The process of parsing is really just taking some input and building a parse tree out of it. That input could be many different things, like a string, sentence, expression, or even an entire program.
Regardless of what input we give it, our parser will parse that input into grammatical phrases and building a parse tree out of it. The parser really has two main roles in the context of our computer and the compilation process:
- When given a valid sequence of tokens, it must be able to generate a corresponding parse tree, following the syntax of the language.
- When given an invalid sequence of tokens, it should be able to detect the syntax error and inform the programmer who wrote the code of the problem in their code.
And that’s really it! It might sound really simple, but if we start considering how massive and complex some programs can be, we’ll quickly start to realize how well-defined things need to be in order for the parser to actually fulfill these two seemingly easy roles.
For example, even a simple parser needs to do a lot in order to process the syntax of an expression like 1 + 2 + 3 x 4.
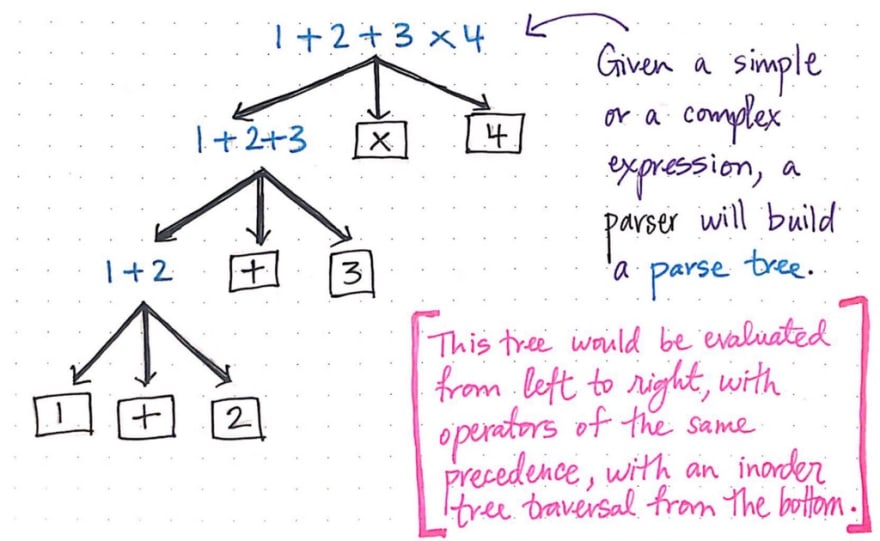
- First, it needs to build a parse tree out of this expression. The input string that the parser recieves might not show any association between operations, but the parser needs to make a parse tree that does.
- However, in order to do this, it needs to know the syntax of the language, and the grammar rules to follow.
- Once it can actually create a single parse tree (with no ambiguity), it needs to be able to pull out the tokens and non-terminal symbols and arrange them so that the parse tree’s heirarchy is correct.
- Finally, the parser needs to ensure that, when this tree is evaluated, it will be evaluated from left to right, with operators of the same precedence.
- But wait! It also needs to make sure that, when this tree is traversed using the inorder traversal method from the bottom, not a single syntax error ever occurs!
- Of course, if it does break, the parser needs to look at the input, figure out where it will break, and then tell the programmer about it.
If this feels like an awful lot of work, that’s because it is. But don’t worry too much about doing all of it, because that’s the parser job, and most of it is abstracted away. Luckily, the parser has some help from other parts of the compiler. More on that next week!
Resources
Lucky for us, compiler design is something that is well-taught in almost every computer science curriculum, and there are a decent number of solid resources out there to help us understand the different parts of a compiler, including a parser and the parse tree. However, as is the case with most CS content, a lot of it can be hard to digest — particularly if you’re not familiar with the concepts or the jargon that’s used. Below are some more beginner-friendly resources that still do a good job of explaining parse trees if you find yourself wanting to learn even more.
- Parse Tree, Interactive Python
- Grammars, Parsing, Tree Traversals, Professors David Gries & Doug James
- Let’s Build A Simple Interpreter, Part 7, Ruslan Spivak
- A Guide to Parsing: Algorithms and Terminology, Gabriele Tomassetti
- Lecture 2: Abstract and Concrete Syntax, Aarne Ranta
- Compilers and Interpreters, Professor Zhong Shao
- Compiler Basics — The Parser, James Alan Farrell



Top comments (3)
This was great. You explained the basis of my college computer language class in one well-written article!
Cheer for that, never done a CS degree so parse tree and how compilers work is not something I know. The compiler is basically a parser?
Awesome! Thanks for the read.