A new lightweight lossless compression scheme

Hi, everyone!

Recently, I’ve been researching lightweight compression and approximate computing in data streams. During this time, I’ve found a simple lightweight compression algorithm. To my knowledge, it hasn’t been proposed before.

---

Compression is used heavily in databases to improve performance. Lightweight compression algorithms are usually very simple and hardware-friendly. For lightweight compression schemes, there’s a great comprehensive survey by the researchers at TU Dresden.

In short, there aren’t many lightweight compression schemes:

1. Frame of reference
2. Delta encoding
3. Dictionary compression
4. Run-length encoding
5. Null suppression

They are all very simple, lightweight, and fast compared to more generic compression algorithms like LZW. Lightweight schemes can even get better compression ratios in some scenarios.

Frame of reference is quite interesting. It was originally proposed to compress database indexes. The claim is that there are cases when the dynamic range of data is quite small. For example, in stocks, we don’t expect to see big changes in a short period of time. We may get something like:

[100, 101, 102, 102, 101, 104, 105]

Using frame of reference compression, we take the minimum value in some block, which will be our “reference”, and then we represent the rest of the numbers as the difference to that reference value. The data will now look like:

[100, 1, 2, 2, 1, 4, 5]

The hope is that the differences to the reference value requires less space to store than the original values (e.g. int64_t to int8_t).

---

In signal processing and IoT, data volumes are large while IoT devices are small and low-power. To address these issues, approximations can be used.

One class of techniques is piecewise approximation, which segments the data stream and approximates each segment.

Some techniques here include:

1. Adaptive piecewise constant approximation
2. Piecewise linear approximation
3. Discrete wavelet transform

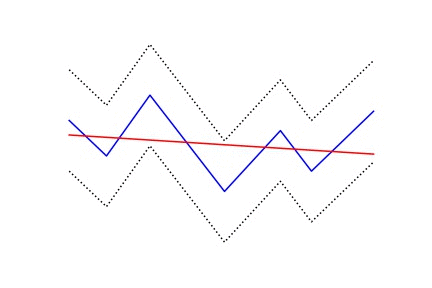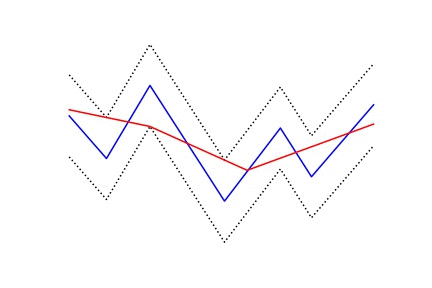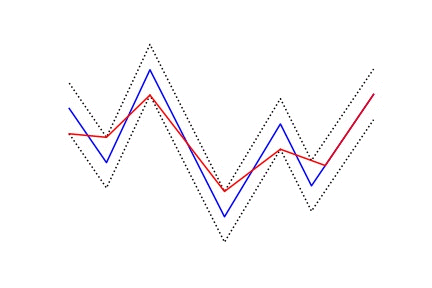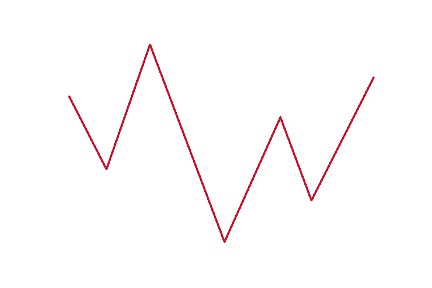
The one I took particular interest in was PLA (piecewise linear approximation). There are fast O(N) algorithms to segment a stream and find an approximation such that the approximation differs no more than a given maximum error threshold. And while the algorithm cannot be vectorized, it is embarrassingly parallel.

Here is an animation that may give some intuition on how it works.

---

With this info in mind, I came up with a new lightweight compression scheme. It’s so simple that it’s certainly not new.

The algorithm is simple and very straightforward:

1. Run piecewise linear approximation and set the maximum error to something that will fit in, say, int8_t
2. Record the differences between the approximation and the actual value, which is guaranteed to fit in int8_t

That’s it! It’s really that simple. There is a little bit of tweaking that needs to be done so that the PLA algorithm can support integers, but that is also quite straightforward. Both compression and decompression is embarrassingly parallel. While compression is not vectorizable, decompression is. It can also be combined with other techniques such as run-length encoding or delta encoding to compress even further.

Thanks for reading!

---

References

1. Compressing Relations and Indexes
2. From a Comprehensive Experimental Survey to a Cost-based Selection Strategy for Lightweight Integer Compression Algorithms
3. Online piece-wise linear approximation of numerical streams with precision guarantees

Comments

[Stefan Neidig]

Is there a sample application? Looks interesting. But it is hard for me to grasp it. Would be much easier with a repository showing some implementation details :)

Also: Awesome to see that these findings are from the TU Dresden. Studied IT at TU Dresden for 3 years :D