8.4 Power Set

NB: This post is a part of the series of solving the challenges from 'Cracking The Coding Interview' book with JavaScript. I'll post only the challenges I've figured out on my own - and will try to describe my reasoning behind the solution. Any ideas on how to solve it differently or in a more optimal way are very welcome 😊

Write a method to return all subsets of a set.

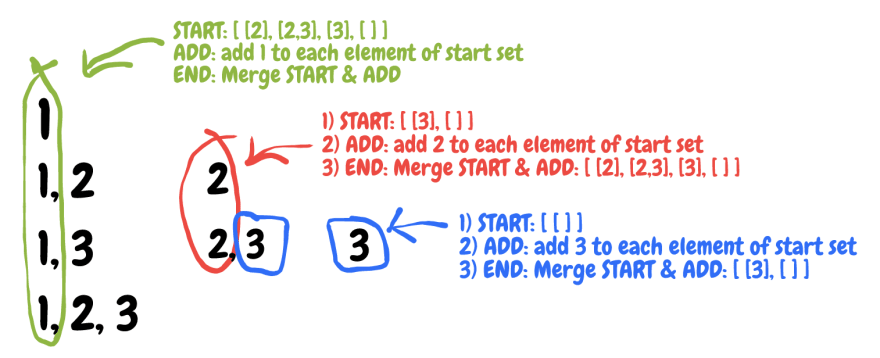
So, what exactly is meant under all subsets of a set? According to Wikipedia's definition of the power set, given an array [1,2,3], the method should return an array of all the possible combinations of the elements of that array + an empty array: [[], [1], [2], [3], [1,2], [1,3], [2,3], [1,2,3]]. After drawing it on the paper, I observe a certain pattern for adding each next number:

Basically, with every next element n of the given array we need to add to the resulting array a copy of all already stored combinations with n added to each. We can turn this logic into the code:

function allSubsets(arr){
  const maxIndex = arr.length - 1; 
  let result = [ [] ];
  arr.forEach(el => {
   result.forEach(subset => {
     result.push([...subset, el]);
   })
  })
  return result;
}

An alternative recursive solution using the same logic will look like:

function allSubsets(arr) {
  if (arr.length === 0) { return [ [] ]; }
  const prev = allSubsets(arr.slice(1));
  const next = prev.map(el => [...el, arr[0]]);
  return [...prev, ...next];
}

So, to get all subsets of array [n...k] (where n and k are min and max index), we will need to:

1) calculate all subsets of array [n+1...k]
2) create a copy of 1)
3) Add n to each subset of a copy
4) Merge 1) and 3)