Maximum Subarray, Kadane's algorithm

Question: Given an array, find the maximum subarray sum.

Eg: For given array : [-2,1,-3,4,-1,2,1,-5,4]
output : 6 for subarray [4,-1,2,1]

Brute force: O(n^2)

Brute force solution would be to go generate all possible subarray and find the maximum subarray.

var maxSubArray = function(nums) {
    if(nums.length == 0) return 0;
    let max = nums[0];
    for(let i=0;i<nums.length;i++){
        let sum = 0;
        for(let j=i;j<nums.length;j++){
            sum+=nums[j];
            if(max<sum) max = sum;
        }
    }
    return max;
};

Now let's observe and find patterns that might help us optimize our solution.

For an Array A let's consider the following observations
If for subarray Sum(A[i,....,j-1]) < A[j], then we know that there's no need to calculate Sum(A[i+1....,j-1]) again since it will definitely be less than A[i].

So based on this, if we come across a situation where current element is greater than sum of previous elements, then we shall start a new subarray from the current subarray.

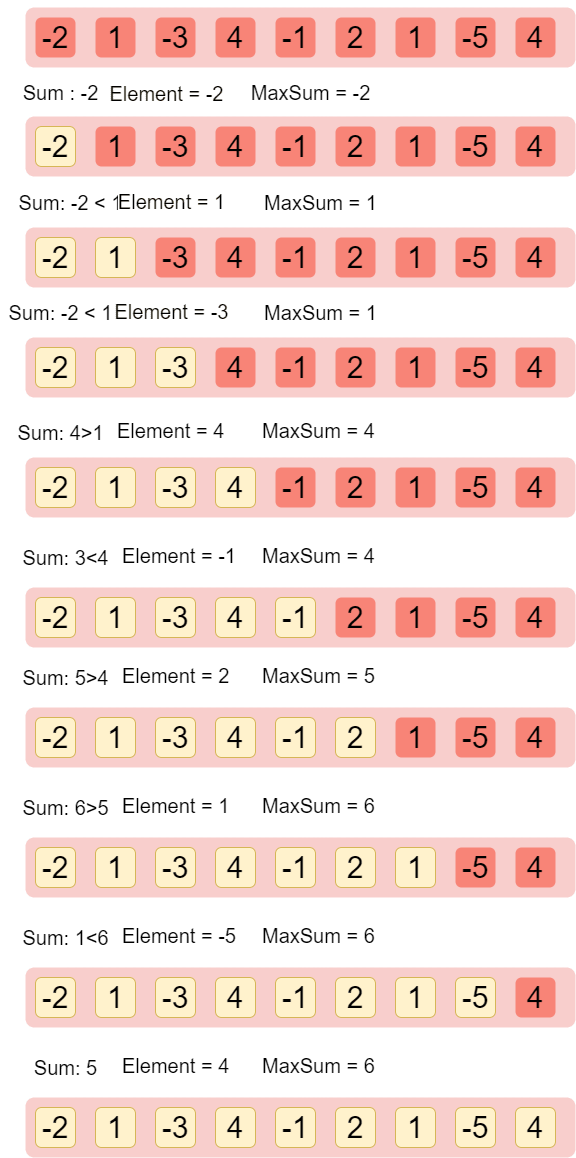
Let's understand this :

So as you can see here,
1 > we maintain two containers, sum and maxSum, we keep on adding elements to sum and compare it with maxSum, and change maxSum only if sum>maxSum.
2 > we change sum when the current element is greater than sum.

this approach improve our time from O(n^2) to O(n).

code:

var maxSubArray = function(A) {
    let sum = A[0];
    let maxSum = A[0];
    for(let i=1;i<A.length;i++){
        sum = Math.max(sum+A[i],A[i]);
        maxSum = Math.max(maxSum,sum);
    }
    return maxSum;
};

github : https://github.com/AKHILP96/Data-Structures-and-Algorithms/tree/master/problems