O(n ) : Don't be a Square

Getting more complex

So far we've covered O(1) aka Constant Time, and O(n) aka linear time.

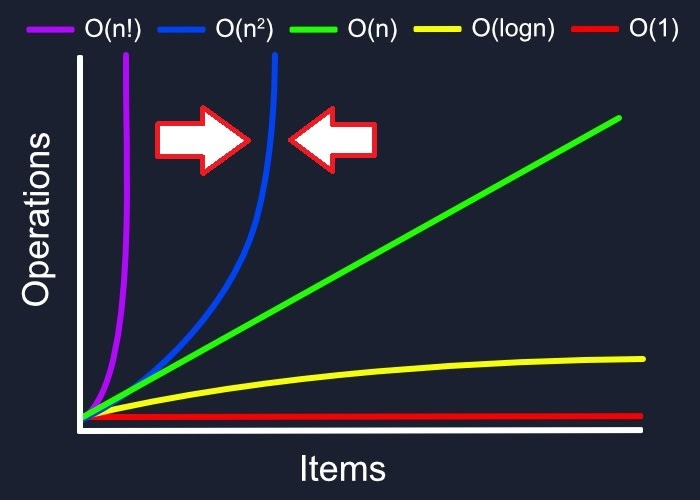
While constant time is the most efficient, linear time is also not bad when it comes to algorithm complexity. O(n²), however, is pretty bad. We'll see just how quickly the operations get out of hand by going back to our catering company...

Our Catering Company is in Trouble

The company that we've been working with were happy with our first event, but they have gotten tons of complaints about our last catering job. Apparently, the guests thought our ingenious Constant Time Soup was lazy and they wanted more food options.

We could try to find a compromise between the two, to deliver a nice experience at better than linear time...

Or we could be super vindictive and hatch a ridiculously contrived revenge plot!

A "Catering Company" Company

If those guests knew how hard it was to run a catering company, they would understand why we wanted to use Constant Time Soup. If they had to make all those meals, they'd recognize our ingenuity.

So we're going to run a new company that teaches people the difference between doing the event each way! That'll teach 'em!

Just like before, let's make some pseudocode to map this out:

# n = number of people aka haters

def teach_those_haters_a_lesson (n)

   # we have to teach each hater 
   n.each do |hater|  # O(n)

     # First we have to get each hater to cater a party
     # for all the other haters, using the individual meal method

     idnv_meal_cater_party(all_the_other_haters) # O(n)

     # After that, we let them do the soup way
     # so they can see why it's better!

     soup_cater_party (all_the_other_haters) # O(1)

   end
end

If that plan sounds like an overly impractical and overly complex plan, you're absolutely right. Not only are we going to have to cater a party with individual meals, we're going to have to do that for every guest! A WHOLE SEPERATE PARTY FOR EVERY GUEST!

Yeah we'll have to also do a soup party, and technically we don't have to make a meal for our revenge victim while they are cooking with us, but those are trifles compared to the extra work we'll do (and remember what happens to constants in big O notation) .

The simplest way to think of it, is that For every guest, we have to make a meal for [almost] every guest. In other words, perform an O(n) complexity algorithm (make meals) O(n) times. Since it's O(n) X O(n), we get O(n²).

Identifying O(n²)

An easy way to spot an O(n²) time complexity are nested loops. Specifically, if a data set is being iterated over within another iteration.

That being said, not every nested iteration results in O(n²) time. The nested loop doesn't have to be correlated with the original input size. For example, if we consider each character in an array of strings, in one case we are looking at the size of the array (how many strings) and in the other we are looking at each string's length (which could be anything).

Since those two inputs aren't necessarily the same, they'll need separate variables, and our big-O function will end up being O(nk) where k represents the size of the other input (in the example case, it would be the max length of an individual string)

If k is constant (or has a maximum value that is constant) then our nested loop would technically simplify to linear time O(n). But, the smaller the size of the input, the more effect it will have. Just because k may become negligible as n reaches infinity, it can still make a big difference at the sizes you're actually inputting.

Next Time

We're almost done with the common complexities. Next time we'll look at logarithmic time O(log n), and it's cousin O(n log n)

Till then...