⚙️ Easy Binary Search Template in Javascript

🏁 Introduction

After finishing 250 questions in LeetCode, I experienced difficulty when I solved the binary search problem. As a human being, I forgot how to write a binary search code. The concept was inside my head, but it was confusing when I should move the left or right index when we fulfilled the condition. Therefore, I took my time to re-learn the binary search and found the key point of binary search on algorithm questions.

🚩 Binary Search Recap

I want to share these two resources that I love to understand Binary Search. One is video and one is text, so you can choose which one you like.

https://www.programiz.com/dsa/binary-search

If you are watching the video, Fireship mentioned about binary search is similar to opening a dictionary. I want to you keep in mind about of that concept.

Key points of binary search:

1. only works on sorted list or array
2. uses two pointers plus a middle index
3. time complexity is O(log n) faster than O(n) / linear

I created a simple case for searching.

You are given arr is a sorted array and k the target value that you need to find the index of the target. If the number is not found, return -1.

arr = [1,3,4,5,7,9];
k = 3;

function search(arr, k){
 let left = 0;
 let right = arr.length - 1;

 while (left <= right) {
   const mid = Math.floor((left + right) / 2);
   if (arr[mid] === k) {
     return mid;
   } else if(arr[mid] < target) {
     left = mid + 1;
   } else {
     right = mid - 1;
   }
 }
}

return -1;

Hopefully, these steps will make it easier to understand the step.

1. First Loop
   

2. Second Loop
   

3. Third Loop
   

I wish at this point, you already understand the main concept of binary search. Let's go deeper to understand the code.

Two Pointers

Make sure you have two variables ready for pointers. I usually use left or right because I'm thinking of an array and it's diagonal. Some people use low or high too.

 let left = 0;
 let right = arr.length - 1;

Iterative

I used left <= right, so the loop will stop when the left pointer is bigger or crosses the right pointer

while (left <= right) {
// ...
}

Let's change the target to be 2, so the last step of the previous example will be like this.

Middle Index

Don't forget about the middle index. It's a must!
We can just sum left and right and divide by 2.
Also, we need to add the Math.floor() because the sum will not always even, so in order to prevent the decimal we can do round down the sum

const mid = Math.floor((left + right) / 2);

Moving the pointers

Okay, the last part of the binary search step. This is why you need strong logic and an understanding of the problem.
Keep in mind you need to move the pointer, so you can reach your answer.

   if (arr[mid] === k) {
     return mid;
   } else if(arr[mid] < target) {
     left = mid + 1;
   } else {
     right = mid - 1;
   }

There are three conditions here.

1. Number is found, so we can just return it (easy)
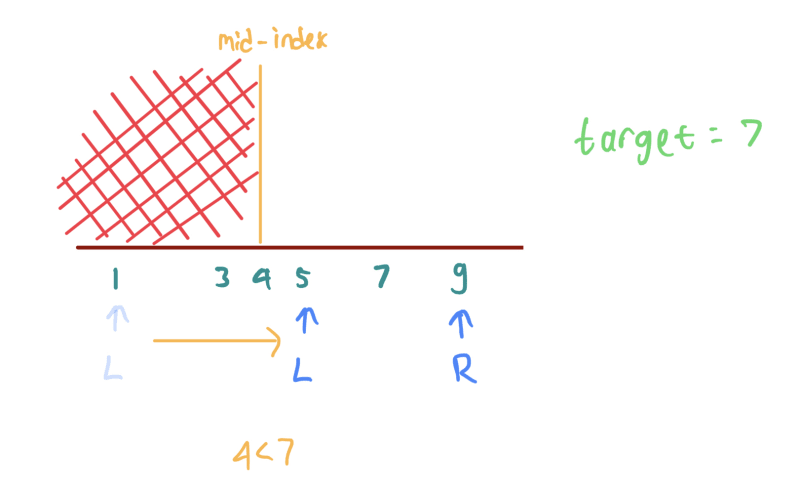
2. Moving the left index closer to the right index. The condition when the mid-index number is smaller than the target.
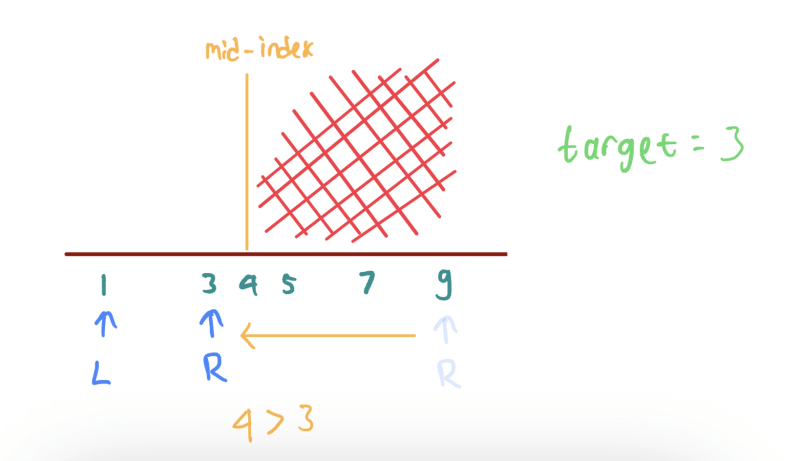
3. Moving the right index closer to the left index. The condition when the mid-index number is bigger than the target.

🏁 Conclusion

This is the time to tap your back and say a great job to yourself. I hope these steps can help you to understand the binary search concept and try to implement it. There is another blog for this series because you could utilize binary search to find the minimum or maximum value. I will create another blog specifically for those cases.

Happy Reading and Good Luck!

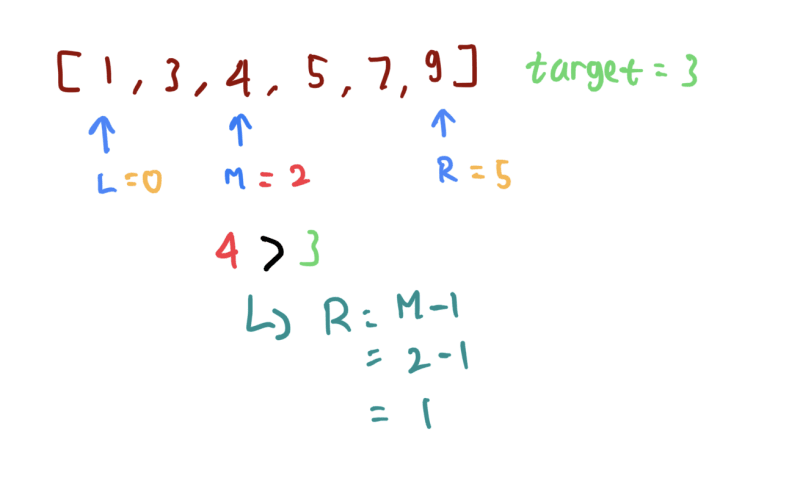
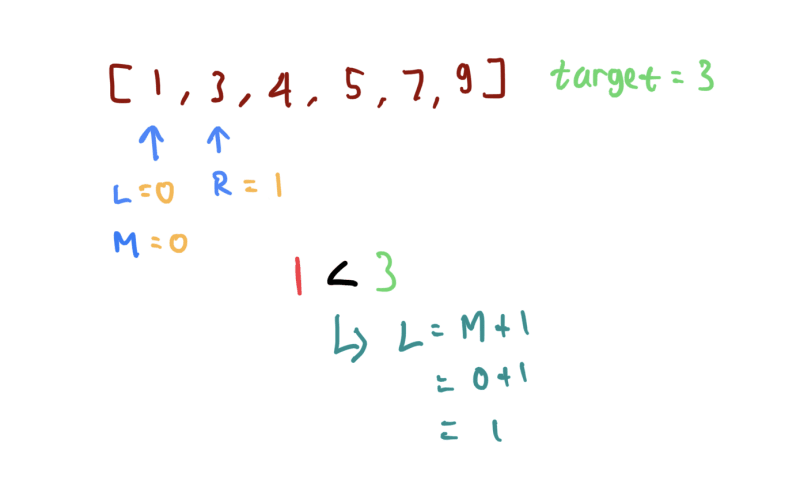
Comments

[Sharmila kannan]

Nice explanation Raynaldo😊

[Gema Anggada]

awesome ray!🔥