Algorithm Optimisation: A Real Example

This post originally appeared on steadbytes.com

In an interview, I was asked to analyse the complexity (and thus relative performance)
of a piece of C code extracted from functioning production software. As a follow up, I will demonstrate the process of identifying a performance problem and implementing a solution to it.

The code had originally been given as part of a pre-interview exam, where general issues with the code were to be discussed. I won't be posting solutions to the pre-interview exam question (there will be potential problems with the code) and I have changed the structure of the code so it's not searchable for future candidates. However, the core algorithm represents an interesting 'real world' optimisation problem to focus on in this post.

Original read_file Algorithm

As the name suggests, read_file reads a file from disk into memory; storing the data in
an array and returning the total number of bytes read:

#include <unistd.h>
#include <fcntl.h>
#include <string.h>
#include <stdlib.h>

#define BUFSIZE 4096

size_t read_file(int fd, char **data)
{
    char buf[BUFSIZE];
    size_t len = 0;
    ssize_t read_len;
    char *tmp;

    /* chunked read from fd into data */
    while ((read_len = read(fd, buf, BUFSIZE)) > 0)
    {
        tmp = malloc(len + read_len);
        memcpy(tmp, *data, len);
        memcpy(tmp + len, buf, read_len);
        free(*data);
        *data = tmp;
        len += read_len;
    }
    return len;
}

Algorithmic Complexity

read_file has O(n²) space and time complexity caused by the memcpy
operations within the while loop:

while ((read_len = read(fd, buf, BUFSIZE)) > 0)
{
    /* allocate space for both existing and new data */
    tmp = malloc(len + read_len);
    /* copy existing data */
    memcpy(tmp, *data, len);
    /* copy new data */
    memcpy(tmp + len, buf, read_len);
    free(*data);
    *data = tmp;
}

All previously read data is copied into a new array in each iteration:

+-+
| |
+-+
 | copy existing data
 v
+-+   +-+
| |   | |
+-+   +-+
 |     |
 v     | read new data
+--+   |
|  | <-+
+--+
 |
 v
+--+   +-+
|  |   | |
+--+   +-+
  |     |
  v     |
+---+   |
|   | <-+
+---+
 |
 v
+---+    +-+
|   |    | |
+---+    +-+
  |       |
  v       |
+----+    |
|    | <--+
+----+

...

Identifying a Performance Problem

Finding the complexity of an algorithm is great to get a relative idea of it's performance will scale with input size. However this is not the same as real world run time; an O(n²) algorithm may not be an issue if it only ever receives small input, for example. Before beginning optimisation the code under question should always be benchmarked and/or profiled. This helps to identify if a problem actually exists and whether a proposed solution is effective.

"The real problem is that programmers have spent far too much time worrying about efficiency in the wrong places and at the wrong times; premature optimization is the root of all evil (or at least most of it) in programming"

-- Donald Knuth, The Art of Computer Programming

The main entry point to the program simply uses read_file to read from standard input and prints the total number of bytes read:

#include <stdio.h>
#include <unistd.h>
#include <fcntl.h>
#include <string.h>
#include <stdlib.h>

#define BUFSIZE 4096

size_t read_file(int fd, char **data);

int main(int argc, char *argv[])
{
    char *data = NULL;

    size_t len = read_file_improved(STDIN_FILENO, &data);

    printf("%ld\n", len);

    return 0;
}

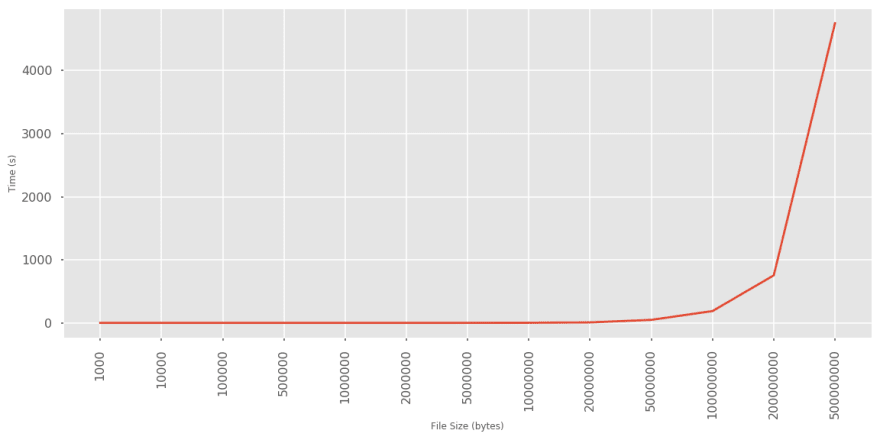
Running the program with randomly generated text files of increasing size clearly demonstrates the O(n²) complexity:

An input size of 0.5Gb takes over an hour to complete!

Improved Algorithm

The issue with read_file is the repeated copying of data - copying each byte only
once would give O(n) complexity. Using a linked list, pointers to each chunk read from the file can be stored in order; creating a new node in each iteration of the loop. After the loop terminates, the linked list can be traversed once and all chunks copied in the final data array. In pseudocode:

typedef struct node_t
{
    char *data; /* chunk of data read from file */
    int len; /* number of bytes in chunk */
    struct node_t *next; /* pointer to next node */
} node_t;

size_t read_file_improved(int fd, char **data)
{
    char buf[BUFSIZE];
    ssize_t read_len;
    size_t len = 0;

    /* build linked list containing chunks of data read from fd */
    node_t *head = NULL;
    node_t *prev = NULL;
    while ((read_len = read(fd, buf, BUFSIZE)) > 0)
    {
        node_t *node = malloc(sizeof(node_t));
        node->data = malloc(read_len);
        memcpy(node->data, buf, read_len);
        node->len = read_len;
        node->next = NULL;

        /* first chunk */
        if (head == NULL)
        {
            head = node;
        }
        /* second chunk onwards */
        if (prev != NULL)
        {
            prev->next = node;
        }
        prev = node;
        len += read_len;
    }

    /* copy each chunk into data once only */
    *data = malloc(len);
    char *p = *data;
    node_t *cur = head;
    while (cur != NULL)
    {
        memcpy(p, cur->data, cur->len);
        p += cur->len;
        cur = cur->next;
    }

    return len;
}

Algorithmic Complexity

Building the linked list (assuming constant overhead for node_t structs) is O(n); each byte from the file is read from the file into an array and then never touched again:

    file reads
 +------+------+
 |      |      |
 V      V      V
+-+    +-+    +-+
| | -> | | -> | | ...
+-+    +-+    +-+

• Arrows between boxes represent linked list node pointers

The final step to copy chunks from the linked list into data is also O(n); traversing pointers in the linked list is O(1) and each byte in each chunk is copied once.

Together, that makes O(2n) ~= O(n)

Performance Comparison

To benchmark each implementation, the main entry point is adapted to take an optional --slow argument to toggle between using the improved algorithm by default and the original:

int main(int argc, char *argv[])
{
    size_t len;
    char *data = NULL;
    /* default to improved implementation*/
    if (argc == 1)
    {
        len = read_file_improved(STDIN_FILENO, &data);
    }
    /* optionally specify original implementation for comparison purposes */
    else if (argc == 2 && !strcmp(argv[1], "--slow"))
    {
        len = read_file(STDIN_FILENO, &data);
    }
    else
    {
        fprintf(stderr, "usage: read_file [--slow]\nReads from standard input.");
        return 1;
    }
    /* do some work with data */
    printf("%ld\n", len);

    return 0;
}

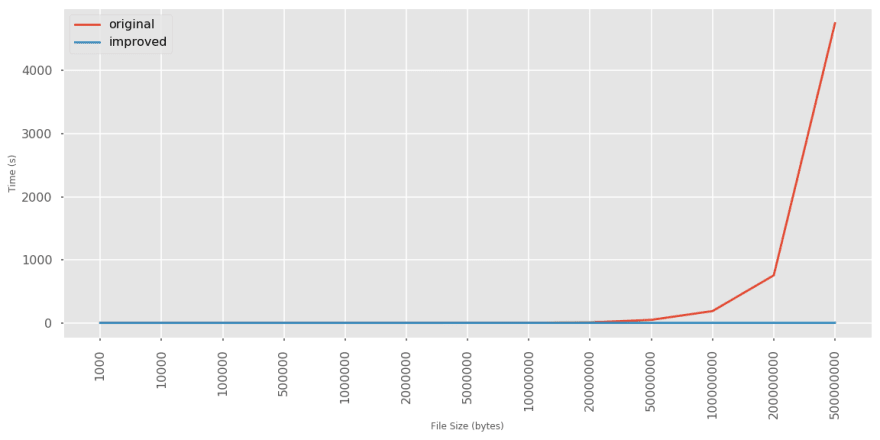
Running the same benchmark of randomly generated text files produces
quite clear results:

Conclusion

Understanding algorithmic complexity is key to implementing well performing programs. However, it should also be coupled with performance benchmarks to avoid premature optimisation. In this post I have demonstrated how to:

• Identify a performance problem
• Determine the complexity of an algorithm
• Re-design an algorithm to be more performant
• Prove the validity of an optimisation

Full code including benchmark script and analysis can be found on GitHub here.

Comments

[ArcticSpaceFox]

Very cool, love to read more :)

[Ben Steadman]

Thanks for reading, I'm glad you liked it! 😊 I'm hoping to do more posts in this area so keep an eye out for more 😉