In the previous article we showed how to draw a regular star polygon which was not degenerate i.e it could be drawn without lifting the pen from the paper. In this one we will attempt to come up with a way to draw two types star polygons.
By two types I mean degenerate (must lift pen) and non-degenerate/regular (no lift pen) but I don't know the true names of these star polygons types. But I hope I get the idea across
Repeated regular polygon method
In this method we are going to look at how to draw a degenerate star polygon by repeatedly drawing regular polygon polygons (like triangles, squares and pentagons)
The Star of David
Let's begin with the simplest degenerate star we know of the Star of David. This type of star can be draw by simply drawing one equilateral triangle and then overlapping it with another one which is upside down
Note that you can draw a triangle using the circle function! See the code below
import turtle as t
t.shape('turtle')
t.color('#4F86F7')
t.pensize(2)
LENGTH=200
t.circle(LENGTH)
t.circle(LENGTH,steps=3)
t.circle(LENGTH,steps=4)
t.circle(LENGTH,steps=5)
In the code above, we are drawing a triangle, square and a pentagon inscribed within the same circle making use of the steps parameter. Here's what we get:
Now we know how to use the steps argument, we can use it twice from two different places on a circle to draw our star
import turtle as t
t.shape('turtle')
t.color('#4F86F7')
t.pensize(2)
LENGTH=200
def star_of_david():
"""Draws two overlapping triangles
"""
t.circle(LENGTH,steps=3)
t.penup()
t.circle(LENGTH, 180)
t.pendown()
t.circle(LENGTH,steps=3)
t.circle(LENGTH)
star_of_david()
In the code above t.circle(LENGTH, 180) makes the turtle go to the top of the circle so that it can draw another triangle from there. Here's what we get
Degenerate Octagram
You can draw a degenerate octagram using a similar method
import turtle as t
t.shape('turtle')
t.color('#4F86F7')
t.pensize(2)
LENGTH=200
def degenerate_octagram():
t.circle(LENGTH,steps=4)
segments=8
t.circle(LENGTH,360/segments)
t.circle(LENGTH,steps=4)
t.circle(LENGTH)
degenerate_octagram()
After drawing the first square, we are moving the turtle to a location determined by 360 / segments. segments = 8 because an octagram has 8 equal segments.
Remember that a n-gram star has n equal segments
Degenerate enneagram
According to wikipedia, enneagram is a 9 pointed star. Unlike the hexagram and the decagram, the enneagram cannot be drawn with just two regular polygons. But how many do we need?
A degenerate enneagram should be drawn by using 3 equilateral triangles (You can try drawing this on a piece of paper too).
import turtle as t
t.shape('turtle')
t.color('#4F86F7')
t.pensize(2)
LENGTH=200
def enneagram():
segments=9
t.circle(LENGTH, steps=3)
t.circle(LENGTH, 360/segments)
t.circle(LENGTH, steps=3)
t.circle(LENGTH, 360/segments)
t.circle(LENGTH, steps=3)
t.circle(LENGTH)
enneagram()
In the code above, we are calling the circle(LENGTH, steps=3 function 3 times
A General method - 1 (Regular non star Polygon based)
Now, how do we know the number of times we need to repeat the circle and step commands? To answer that we can make a few observations about the examples above:
- A hexagram is a (6,2) star where the vertices - 6 is divisible the order- 2, 3 times
- A octagram is a (8,2) star where the vertices - 8 is divisible the order- 2, 4 times
- A enneagram is a (9,3) star where the vertices - 9 is divisible the order- 3, 3 times
With the above, we might be able to say that for a degenerate n-gram with the order m, the quotient of n/m is the number of sides of the polygon while the order m is the number of times we need to draw the polygon
So, we should try the following:
For an n,m degenerate star draw m number of regular polygons
And the polygons drawn should have n/m sides
Let's code that
import turtle as t
t.shape('turtle')
t.color('#4F86F7')
t.pensize(2)
LENGTH=200
def degenerate(n,m):
segments = n
order = m
sides = int(n/m)
for _ in range(order):
t.circle(LENGTH, steps=sides)
t.circle(LENGTH, 360/segments)
t.circle(LENGTH)
degenerate(10,2)
The code above works! It drew the 10 gram and the 12 grams below
| (10,2) | (12,2) |
|---|---|
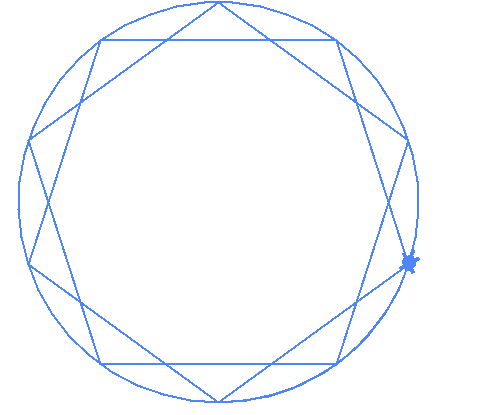 |
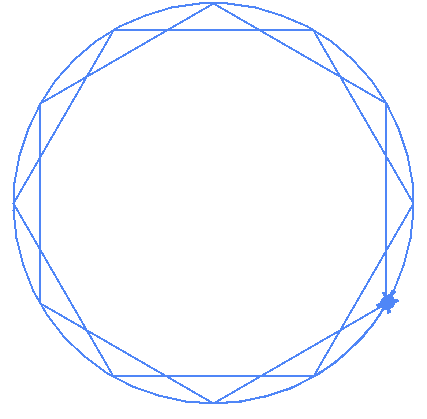 |
You can also draw (12,3) and (12,4)
| (12,3) | (12,4) |
|---|---|
 |
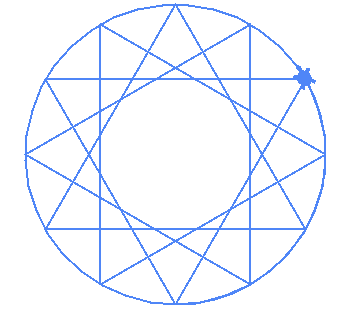 |
Interestingly if you try to draw (10,5) and (12,6) it draws this:
| (10,5) | (12,6) |
|---|---|
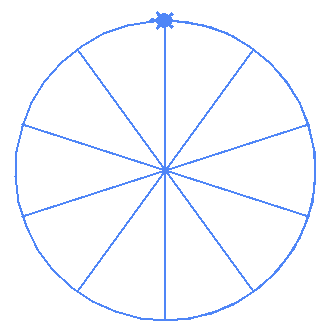 |
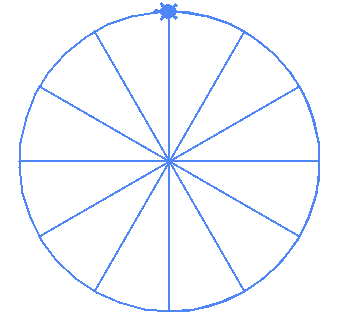 |
This is a reminder that the possible orders (values of m) are
2 through (n-1)/2-1. Basically the order can't be 1 and it also can't be half of the number of vertices
With the general code above, have we covered all the degenerate regular star polygons?
The (10,4) star
In the examples that we have looked at a degenerate star polygon can be composed of multiple regular (non-star) polygons. But (10,4) is a curious case. In the previous article we had written a code that draws regular stars. Let's see what happens when we use it here
import turtle as t
t.shape('turtle')
t.color('#4F86F7')
t.pensize(2)
LENGTH=150
def regular_star(n,m):
""" n = number of pointies
m = order of the star,
(number of skips + 1)
"""
angle = 360*m/n
for count in range(n):
t.forward(LENGTH)
t.right(angle)
regular_star(10,4)
Yes we get a pentagram! But we were supposed to have 10 vertices :(
A new type of degenerate
Hence, (10,4) is a new type of degenerate star where n is not divisible by m and as such we cannot draw it with the degenerate function we wrote earlier.
We can draw this type of degenerate stars by overlapping two stars. Unfortunately we cannot use the circle's step parameter anymore. We need to draw a regular star then rotate it to draw another star. To do that we will first begin by modifying our regular_star function as follows
def regular_star(n,m):
""" n = number of pointies
m = order of the star,
(number of skips + 1)
"""
angle = 360*m/n
t.left(180-angle/2)
for count in range(n):
t.forward(LENGTH)
t.right(angle)
t.right(180-angle/2)
The code above adds t.left(180-angle/2) to place the regular star to the left side of the turtle. This is similar to how a circle command behaves
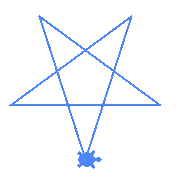 |
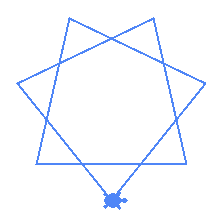 |
Notice above that both the stars are drawn to the left side of the turtle
We will additionally make the following changes to our code
import turtle as t
import math
t.shape('turtle')
t.color('#4F86F7')
t.pensize(2)
RADIUS=150
def regular_star(n,m):
""" n = number of pointies
m = order of the star,
(number of skips + 1)
"""
angle = 360*m/n
center_angle = 2*m*math.pi/n
t.left(180-angle/2)
length=2*RADIUS*math.sin(center_angle/2)
for count in range(n):
t.forward(length)
t.right(angle)
t.right(180-angle/2)
regular_star(7,2)
t.circle(RADIUS)
In the code above, we have made the following changes
- Replaced the global
LENGTHwithRADIUS. This is to allow us to draw the star of a defined radius - Computed a center angle which is the angle subtended by
msegments on the center of the circle.center_angleis the representation of arch length in radians - We used the
center_angleand theRADIUSto compute the length of the arms of the star
| (5,2) | (7,2) | (7,3) |
|---|---|---|
 |
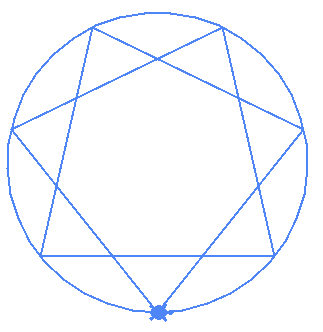 |
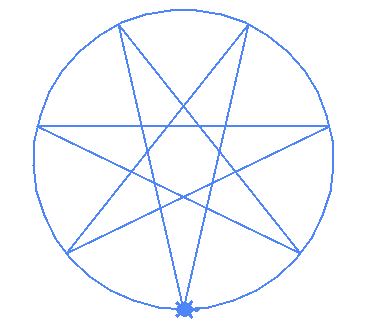 |
We can now draw a star to the left side of the turtle having defined radius. We can even overlap them all
A better general method
Our goal is to build a better general method to draw any degenerate regular polygon star of a given number of vertices and order. Let's begin again by listing the properties of the degenerate stars
| Star | Properties |
|---|---|
| (6,2) | 2 overlapping triangles |
| (8,2) | 2 overlapping squares |
| (9,3) | 3 overlapping triangles |
| (10,4) | 2 overlapping pentagrams |
| (14,4) | 2 (7,2) stars |
| (14,6) | 2 (7,3) stars |
| (15,6) | 3 overlapping pentagrams |
The above can be verified by trying them out on a piece of paper (or by just thinking way too hard)
Here's an algorithm that we might be able to use to draw all the of the above stars
- Find the greatest common divisor (gcd) of
nandm - Divide
nandmby thegcdto obtain a star (n/gcd,m/gcd) - Draw the (n/gcd,m/gcd) star
- Move the turtle to another position on the circumcircle determined by 360/n degrees
- Repeat 3 until we have drawn the star
gcdnumber of times
Let's try it:
import turtle as t
import math
t.shape('turtle')
t.color('#4F86F7')
t.pensize(2)
RADIUS=150
def regular_star(n,m):
""" n = number of pointies
m = order of the star,
(number of skips + 1)
"""
angle = 360*m/n
center_angle = 2*m*math.pi/n
t.left(180-angle/2)
length=2*RADIUS*math.sin(center_angle/2)
for count in range(n):
t.forward(length)
t.right(angle)
t.right(180-angle/2)
def star(n,m):
""" n = number of pointies
m = order of the star,
(number of skips + 1)
"""
gcd = math.gcd(n,m)
new_n = int(n/gcd)
new_m = int(m/gcd)
segment_angle = 360/n
for _ in range(gcd):
regular_star(new_n, new_m)
t.penup()
t.circle(RADIUS, segment_angle)
t.pendown()
star(10,4)
With the code above it turns out that when the gcd is 1, we get either a regular non-degenerate star or a polygon. So we have written code to generalize:
- Regular Polygons
- Regular Non-degenerate stars!
- Regular degenerate stars!~
- Weird stick star :)
Examples:
| Name | Drawing |
|---|---|
| (10,1) | 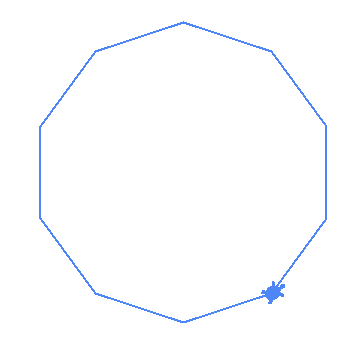 |
| (10,2) | 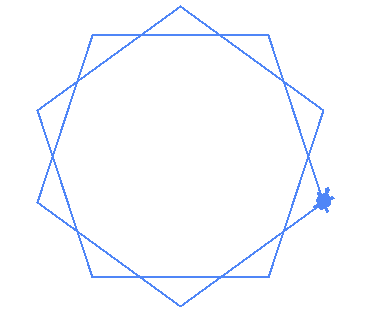 |
| (10,3) |  |
| (10,4) | 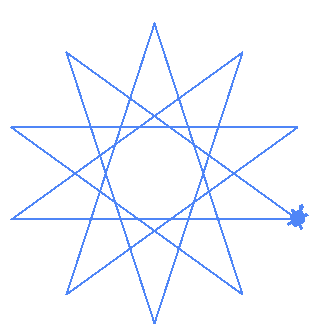 |
| (10,5) | 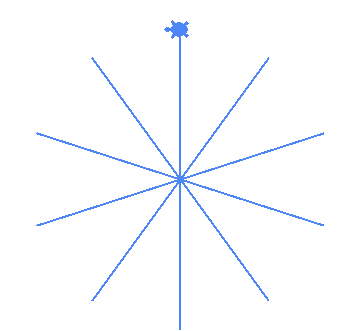 |
| (14,4) | 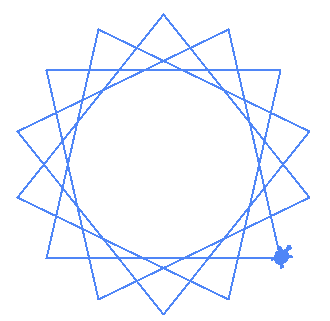 |
| (14,6) | 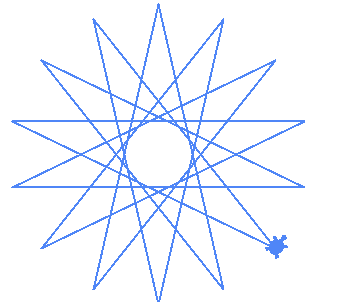 |
| (15,6) | 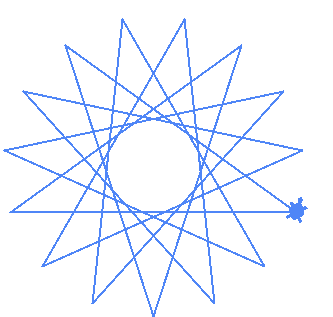 |
Bonus
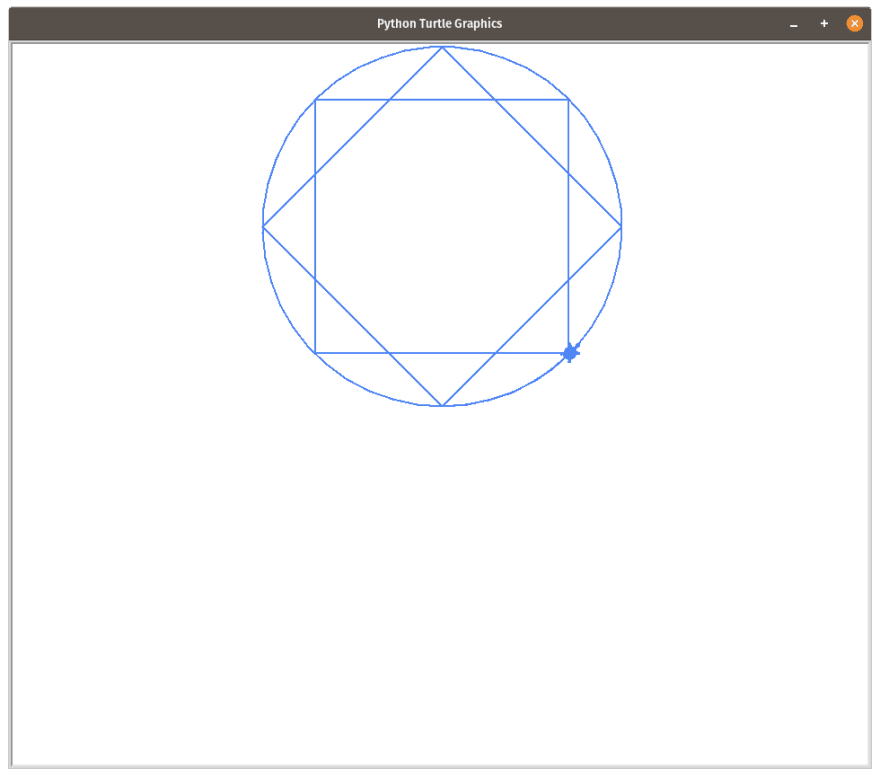
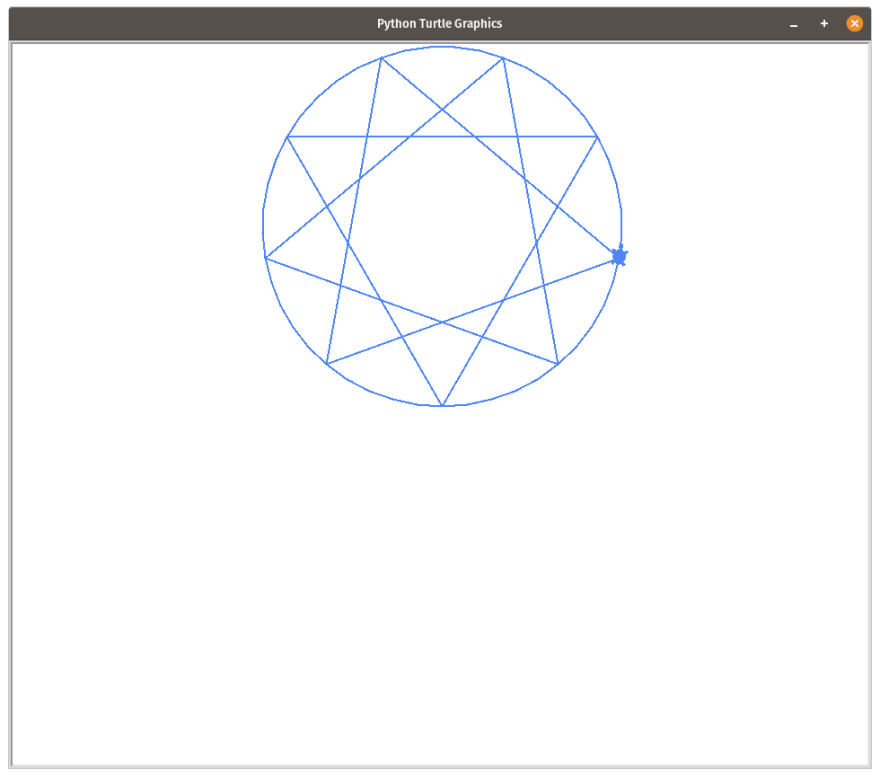
You can overlap all orders for a fixed number of vertices to get beautiful images such as these
def all_stars(n):
for x in range(int(n/2)):
star(n,x+1)
all_stars(10)
t.hide()
Yay!!~









Top comments (0)