I've been learning a lot about data structures and algorithms lately and I've noticed in my reading that there aren't a lot of examples showing implementations of algorithms in Javascript. You'll mostly find examples in Java, Python, C, C++ etc. Maybe there's a reason for preferring these languages over Javascript? I'm not sure.
In this first part, I'm going to show Javascript implementations of three sorting algorithms:
- Merge sort
- Insertion sort
- Bubble sort
This is not intended to be an in-depth explanation on the ins and outs of how the algorithms work and their performance. If you'd rather read about that, here's a nice resource I found: Sorting Algorithms
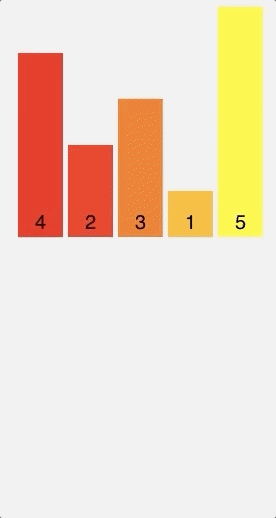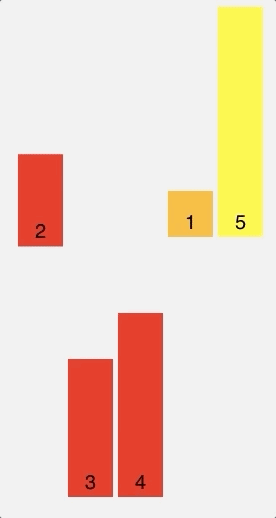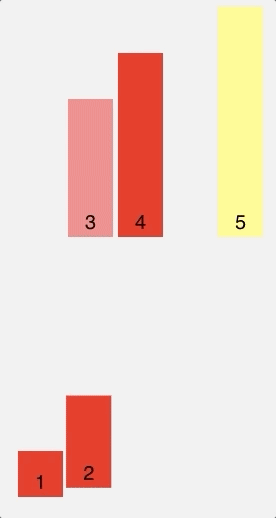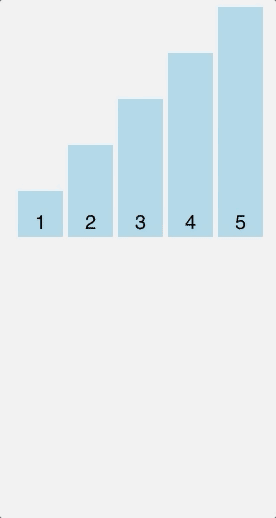
To keep things simple, I'll be sorting a simple list list having only 5 elements [4, 2, 3, 1, 5].
Merge Sort
Merge sort uses a divide-and-conquer approach to sort elements in an array. Basically, what this means is that instead of dealing with the array as a whole, it continually splits it in half until both halves are sorted, then the halves are merged into one solved list.
Visual
Code
function mergeSort(list) {
const len = list.length
// an array of length == 1 is technically a sorted list
if (len == 1) {
return list
}
// get mid item
const middleIndex = Math.ceil(len / 2)
// split current list into two: left and right list
let leftList = list.slice(0, middleIndex)
let rightList = list.slice(middleIndex, len)
leftList = mergeSort(leftList)
rightList = mergeSort(rightList)
return merge(leftList, rightList)
}
// Solve the sub-problems and merge them together
function merge(leftList, rightList) {
const sorted = []
while (leftList.length > 0 && rightList.length > 0) {
const leftItem = leftList[0]
const rightItem = rightList[0]
if (leftItem > rightItem) {
sorted.push(rightItem)
rightList.shift()
} else {
sorted.push(leftItem);
leftList.shift()
}
}
// if left list has items, add what is left to the results
while (leftList.length !== 0) {
sorted.push(leftList[0])
leftList.shift()
}
// if right list has items, add what is left to the results
while (rightList.length !== 0) {
sorted.push(rightList[0])
rightList.shift()
}
// merge the left and right list
return sorted
}
const list = [4, 2, 3, 1, 5]
const sorted = mergeSort(list)
console.log(sorted)
Insertion Sort
Insertion sort builds the final sorted list one element at a time. It does this by taking one element, comparing it to the rest of elements in the list, finding its right position, and then placing it there.
This is known as comparison-based sorting.
Visual
Code
function insertionSort(list) {
const len = list.length
for (let i = 1; i < len; i++)
{
if (list[i] < list[0])
{
// move current element to the first position
list.unshift(list.splice(i,1)[0])
}
else if (list[i] > list[i-1])
{
// maintain element position
continue
}
else {
// find where element should go
for (let j = 1; j < i; j++) {
if (list[i] >= list[j-1] && list[i] <= list[j])
{
// move element
list.splice(j, 0, list.splice(i,1)[0])
}
}
}
}
return list
}
const list = [4, 2, 3, 1, 5]
const sorted = insertionSort(list)
console.log(sorted)
Bubble Sort
Another example of a comparison-based sorting algorithm, Bubble sort compares each pair of elements in a list and swaps them if they are out of order until the list is sorted.
Visual
Code
function bubbleSort(list)
{
let swapped
let n = list.length-1
do {
swapped = false
for (let i=0; i < n; i++)
{
// compare pairs of elements
// if left element > right element, swap
if (list[i] > list[i+1])
{
const temp = list[i]
list[i] = list[i+1]
list[i+1] = temp
swapped = true
}
}
}
// continue swapping until sorted
while (swapped)
return list
}
const list = [4, 2, 3, 1, 5]
const sorted = bubbleSort(list)
console.log(sorted)
Thats it! 😊 And, incase you're wondering, I used this site to make the visuals.
In the next part, I'll be going through:
- Quick sort
- Heap sort
- Counting sort





Top comments (10)
Hello there! First let me thank you for the article, it helped me a lot. As I was developing an insertion sort I came across your code and used it, although you have a litle mistake I ended up finding.
instead of:
if (list[i] > list[j-1] && list[i] < list[j])
you should have (= is missing on second validation):
if (list[i] > list[j-1] && list[i] =< list[j])
Otherwise, it wont sort. Once again, thank you!
Hey there! I'm glad you found it helpful. Thanks for that 😄.
The code seems to work just fine with the test list provided though. Would you mind explaining why the
=is necessary? Or maybe share the list you tested the code with so I can also try it.Ps: The
=should be on the other side of the<in your example though, like so:if (list[i] > list[j-1] && list[i] <= list[j])🙂Hey Kinyanjui, thanks again for the post! Super helpful!
Just hoping on to this, I noticed an issue with the same line of code where if a list has two elements with the same value it won't sort it properly. i.e.
[4, 2, 3, 2, 1, 5]gives[ 1, 2, 3, 4, 2, 5 ]as a result.Adding an
=sign to the first argument makes all the difference!if (list[i] >= list[j-1] && list[i] < list[j]). It now returns[ 1, 2, 2, 3, 4, 5 ]:)Thanks Lynn. I've edited the code to include your fix.
Hello guy ! Nice post !
What is the faster sort algorithm ? Is it depends of number of elements ?
Thanks for reading!
In this case, Merge sort is the faster of the three with time complexity O(nlogn). Time complexity (the estimated time taken by running an algorithm) is measured by how many operations are executed so yes, the number of elements will matter, but not as much as the order of the elements:
Nice Article. Thanks for taking the time to write this :)
Thanks for taking the time to read Aditya :)
Hey, nice overview. One thing though. Merge sort is also comparison based. To sort in the end, you always compare two elements.
Nice catch! Thanks