What is Sorting
Sorting - ordering a list of data items in a pre-defined sequence
Sorting algorithms are a set of instructions that take an array or list as an input and arrange the items into a particular order.
Sorts are most commonly in numerical or a form of alphabetical (called lexicographical) order, and can be in ascending (A-Z, 0-9) or descending (Z-A, 9-0) order.
There are many types of sorting algorithms: quick sort, bubble sort, balloon sort, radix sort, merge
sort, quick sort, insertion sort, selection sort, etc. Not one can be considered the fastest because each algorithm is designed for a particular data structure and data set. It would depend on the data set that you would want to sort.
In this post, I will focus on the 5 most commonly used sorting algorithms in Python.
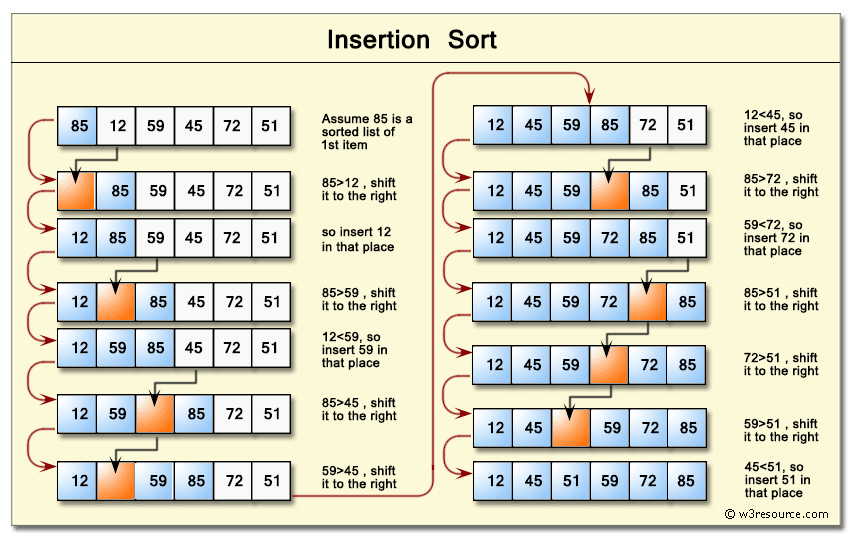
1. Insertion Sort
In Insertion sort, you compare the key element with the previous elements. If the previous elements are greater than the key element, then you move the previous element to the next position.
Usually, start from index 1 of the input array.
def insertion_sort(arr):
'''
insertion sort function that takes an array to be sorted as an input.
With your key element at the index 1 of the input array,
traverse the array comparing the key element with the previous elements.
If the previous element is greater than the key element,
then move the previous element to the next position
'''
l = len(arr)
i=1 #key element index
while i<l:
key_element=arr[i]
j=i-1 #previous element index
while j>=0 and arr[j]>key_element:
# Move elements of arr[0..i-1], that are
# greater than key, to one position ahead
# of their current position
arr[j+1] = arr[j]
j=j-1
arr[j+1]=key_element
i=i+1
return arr
Properties of Insertion Sort
- Space Complexity: O(1)
- Time Complexity: O(n), O(n* n), O(n* n) for Best, Average, Worst cases respectively.
- Sorting In Place: Yes
- Stable: Yes
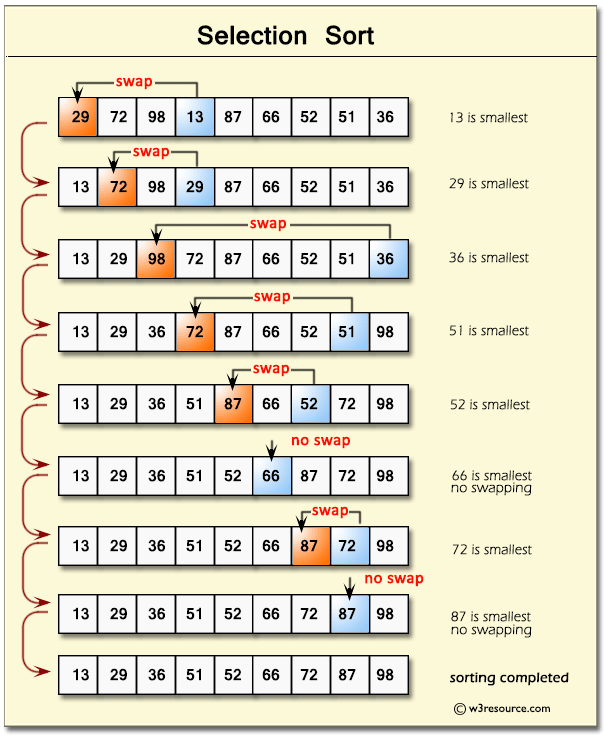
2. Selection Sort
Selection Sort selects the current smallest element and swaps it into place.
Here's how it works:
- Find the smallest element in the array and swap it with the first element. >2. Find the second smallest element and swap with the second element in the array.
- Find the third smallest element and swap wit with the third element in the array.
- Repeat the process of finding the next smallest element and swapping it into the correct position until the entire array is sorted.
def selection_sort(alist):
for i in range(0, len(alist) - 1):
smallest = i
for j in range(i + 1, len(alist)):
if alist[j] < alist[smallest]:
smallest = j
alist[i], alist[smallest] = alist[smallest], alist[i]
return alist
Selection sort Properties
- Space Complexity: O(n)
- Time Complexity: O(n2)
- Sorting in Place: Yes
- Stable: No
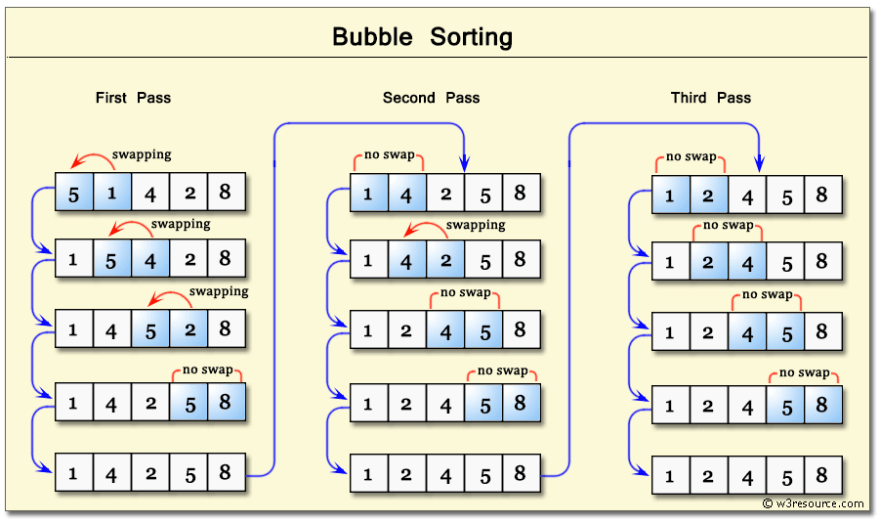
3. Bubble Sort
The algorithm traverses a list and compares adjacent values, swapping them if they are not in the correct order.
def bubble_sort(alist):
n=len(alist)
for i in range(n):
for j in range(i):
if alist[j]>alist[j+1]:
temp = alist[j]
alist[j] = alist[j+1]
alist[j+1] = temp
return alist
Pros
- It is one of the easiest sorting algorithms to understand and code from scratch.
- From technical perspective, bubble sort is reasonable for sorting small-sized arrays or specially when executing sort algorithms on computers with remarkably limited memory resources.
Cons
- Because the time complexity is Ο(n2), it is not suitable for large set of data.
- bubble sort is very slow compared to other sorting algorithms like quicksort.
Selection sort Properties
- Space complexity: O(1)
- Best case performance: O(n)
- Average case performance: O(n*n)
- Worst case performance: O(n*n)
- Stable: Yes
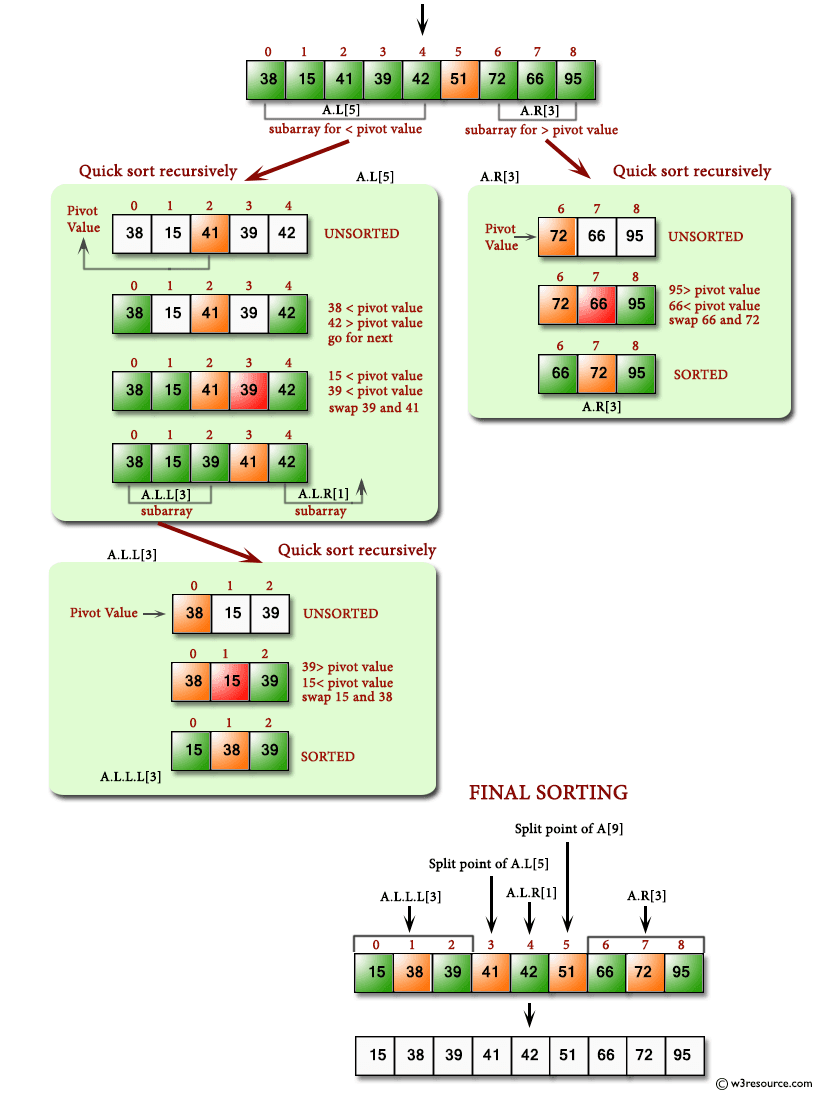
4. Quick Sort
Quick sort uses divide and conquer approach. It divides the list in smaller 'partitions' using 'pivot'. The values which are smaller than the pivot are arranged in the left partition and greater values are arranged in the right partition. Each partition is recursively sorted using quick sort.
The pivot can be the first, the last, the medium or any random element on the array.
The steps involved in Quick Sort are:
- Choose an element to serve as a pivot.
- Partitioning: Sort the array in such a manner that all elements less than the pivot are to the left, and all elements greater than the pivot are to the right.
- Call Quicksort recursively, taking into account the previous pivot to properly subdivide the left and right arrays.
def quicksort(z):
if(len(z)>1):
piv=int(len(z)/2)
val=z[piv]
lft=[i for i in z if i<val]
mid=[i for i in z if i==val]
rgt=[i for i in z if i>val]
res=quicksort(lft)+mid+quicksort(rgt)
return res
else:
return z
Quick sort Properties
- Space complexity: O(n)
- Not stable
- Time Complexity: Best case – nlog(n)
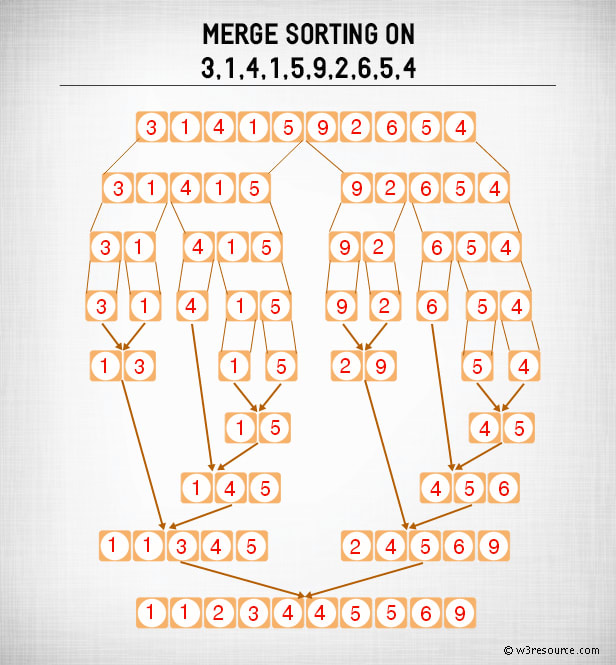
5. Merge Sort
Merge sort is a sorting algorithm based on divide and conquer programming approach. It keeps on dividing the list into smaller sub-list until all sub-list has only 1 element. And then it merges them in a sorted way until all sub-lists are consumed.
def merge(left,right,compare):
result = []
i,j = 0,0
while (i < len(left) and j < len(right)):
if compare(left[i],right[j]):
result.append(left[i])
i += 1
else:
result.append(right[j])
j += 1
while (i < len(left)):
result.append(left[i])
i += 1
while (j < len(right)):
result.append(right[j])
j += 1
return result
def merge_sort(arr, compare = lambda x, y: x < y):
#Used lambda function to sort array in both(increasing and decresing) order.
#By default it sorts array in increasing order
if len(arr) < 2:
return arr[:]
else:
middle = len(arr) // 2
left = merge_sort(arr[:middle], compare)
right = merge_sort(arr[middle:], compare)
return merge(left, right, compare)
Merge sort Properties
- Space Complexity: O(n)
- Time Complexity: O(nlog(n)).
- Stable: Yes
Complexities Summary of Sorting Algorithms
References
Image illustrations adapted from:
https://www.w3resource.com/
https://www.freecodecamp.org/
https://www.geeksforgeeks.org/




Top comments (1)
Correction:
Selection sort space complexity = O(1) in the article.
In Bubble sort, in the second loop, the range is not till 'i' but till 'n-i-1'.