This lesson was originally published at https://algodaily.com, where I maintain a technical interview course and write think-pieces for ambitious developers.

Bitwise Operators and Bit Manipulation for Interviews

Decimal and binary

How do we usually represent numbers? We use decimal notation (a.k.a. Base 10) that provides ten unique digits: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9. To form numbers, we combine these digits in a certain sequence so that each decimal digit represents a value multiplied by a certain power of 10.

For example, in decimal, 152 = 100 + 50 + 2 = 1×10² + 5×10¹ + 2×10⁰.

Decimal numbers are what humans like most. What computers like most are binary numbers (a.k.a. Base 2) where there are only 2 available digits: 0 and 1. As such, a binary number is a sequence of ones and zeros, e.g. 011101001, 1100110, or 110. In a binary number, each digit is referred to as bit, and each bit represents a power of decimal 2.

For humans, reading (and making sense of) binary numbers involves converting them to decimal form. Let's convert the binary number 110 to decimal notation. We know that the three digits in the number represent powers of decimal 2. In order to move from lower to higher powers of 2, we will read binary digits in our number right to left:

(Base 2) 110 = (Base 10) 0×2⁰ + 1×2¹ + 1×2² = 0 + 2 + 4 = 6

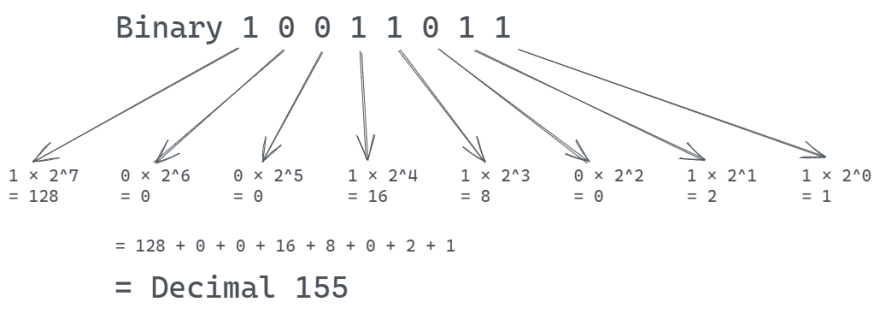
Let's try to convert a larger binary number: 10011000. Remember, we're reading binary digits right to left.

(Base 2) 10011011 = (Base 10) 1×2⁰ + 1×2¹ + 0×2² + 1×2³ + 1×2⁴ + 0×2⁵ + 0×2⁶ + 1×2⁷ = 1 + 2 + 0 + 8 + 16 + 0 + 0 + 128 = 155.

So what's the big deal about binary numbers?

The binary system is a natural fit for electronic circuits that use logic gates, and this is exactly why binary is used internally in all modern computer hardware. (Stock images of entire screens filled with zeros and ones that you see in articles about hackers are silly, yes, but they're not an overstatement.)

Modern high-level programming languages are designed in a way that enables humans to write and read program code, and the heavy lifting necessary to convert program code all the way to machine code is handled by compilers.

That said, most programming languages still provide ways to manipulate data as sequences of bits, as opposed to human-readable values of common types such as numbers and strings.

Although you probably won't see direct bit manipulation used every day (we'll talk about practical uses later), it's good to know how it's done, and it's done with something called bitwise operators.

Enter bitwise operators

A bitwise operator takes one or more values, treats them as sequences of bits, and performs operations on these bits rather than "human-readable" values.

Bitwise operators are available in most programming languages. For our purposes, let's explore how they're implemented in JavaScript.

Bitwise logical operators in JavaScript

JavaScript supports a total of 7 bitwise operators:

• 4 bitwise logical operators: & (Bitwise AND), | (Bitwise OR), ^ (Bitwise XOR), and ~ (Bitwise NOT).
• 3 bitwise shift operators: << (Left shift), >> (Sign-propagating right shift), and >>> (Zero-fill right shift).

JavaScript's bitwise operators treat their operands as binary numbers -- sequences of 32 bits -- but return decimal numbers.

Here's an algorithm that JavaScript's bitwise logical operators follow:

• Operands are converted to 32-bit integers.
• If there are two operands, individual bits from the operands are matched into pairs: first operand's first bit to second operand's first bit, second bit to second bit, and so on.
• The operator is applied to each bit pair, which yields a binary result.
• The binary result is converted back to decimal form.

Possible operands and return values of bitwise operators are often illustrated with something called truth tables. Here's a truth table for all 4 bitwise logical operators available in JavaScript:

a	b	a AND b	a OR b	a XOR b	NOT a
0	0	0	0	0	1
0	1	0	1	1	-
1	0	0	1	1	0
1	1	1	1	0	-

Before we discuss these operators in more detail, let's agree that we can present binary numbers in 3 different ways. Let's take the binary form of decimal 9 as an example:

1. 0000000000000000000000000001001 represents all 32 bits of the number. This form is too long for most cases, but we'll use it when talking about binary shifts.
2. 1001 is the short form for the same number. Here, we include bits from the first bit that is set to 1 through the rightmost bit. We'll use this form in most examples.
3. 0b1001 is the format for expressing binary numbers in JavaScript source code. Apart from the 0b prefix, there's nothing fancy about it. We'll use this form in some code samples.

& (Bitwise AND)

Bitwise AND takes bit representations of its two operands, combines bits in pairs by their order, and applies logical AND to each pair. It returns the resulting bit sequence converted back to its decimal form.

For each bit pair, Bitwise AND returns 1 only if both bits are 1. In all other cases, it returns 0.

Let's see what's going on here. Suppose we want to apply Bitwise AND to two numbers, 13 and 11:

> a & b

What happens when this line is executed?

1. First, the two values are converted from decimal to binary form: 13 represented in binary is 1101, and 11 becomes 1011.

2. Then, each bit of the first number is paired with a corresponding bit of the second number:

   

3. Now, the familiar logical AND is applied to each of the bit pairs:
   

   1101 &
   1011 ==
   
   1001
   

4. After calculating the result, 1001, JavaScript converts it back to the decimal value 9 and returns:
   

   > 13 & 11
   9
   

| (Bitwise OR)

If you understand Bitwise AND, the next two bitwise operators won't come as a surprise. Everything works the same way -- conversion to binary form, pairing bits from two operands, and subsequent conversion of a result to decimal form -- except that to each bit pair, a different operation is applied.

With Bitwise OR, a | b returns 1 if either a or b is 1. Again, think of it as of applying the good-old logical OR (||) to a set of bit pairs.

For example, if we apply Bitwise OR to the same two numbers -- 13 | 11 -- the numbers are first converted to binary form, which results in 1101 and 1011 respectively, and then for each pair, a resulting 1 is returned every time at least one bit in a pair contains a 1:

1101 |
1011 == 

1111

The result, 1111, is converted to decimal form, and the decimal 15 is returned:

> 13 | 11
15

^ (Bitwise XOR)

For any given bit pair, Bitwise XOR (a.k.a. Bitwise exclusive OR) returns 1 only if two bits in the pair are different. In all other respects, it works exactly the same as Bitwise AND and Bitwise OR:

1101 |
1011 == 

0110

~ (Bitwise NOT)

Bitwise NOT is a little different, as it's applied to one operand, not two. What it does is trivial: after converting the operand to binary, it simply inverts its bits.

There's a quirk though. As we said before, before applying bitwise operators, JavaScript converts an operand to a 32-bit sequence. The leftmost bit in this sequence is used to store the sign of the number: 0 in the leftmost bit means positive, and 1 means negative.

Since Bitwise NOT inverts all 32 bits of its operand, it also inverts its sign: negative turns positive, and vice versa.

For example, here's the entire 32-bit sequence representing the decimal 9:

00000000000000000000000000001001

Invoking Bitwise NOT (~9) reverts all bits, which results in:

11111111111111111111111111110110

The leftmost bit now holds 1, which means the number is negative. The negative number is represented in something called 2's complement, and if you want to know how to use it, here's a quick but very solid summary of how it works.

For now, you want to know that the decimal representation of the resulting number is -10. In fact, applying Bitwise NOT to any number x returns -(x + 1). For example, ~9 returns -10, ~-8 returns 7, and so on.

Bitwise shift operators in JavaScript

All bitwise shift operators in JavaScript move individual bits left or right by a number of bit positions that you specify.

<< (Left shift)

Left shift (<<) shifts bits of the first operand to the left. The value of the second operand determines how many positions the bits are shifted. Bits shifted off to the left are discarded. Positions that free up to the right are populated with zero bits.

Let's look at an example: what exactly does 7<<2 do in JavaScript?

1. The first (left) operand is converted to binary form: 7 in binary is 111. In fact, the entire binary number has 32 bits, but the remaining bits to the left are all zeros:
   

   0000000000000000000000000000111
   

2. Because the second operand is 2, two leftmost bits are now stripped off, leaving us with 30 bits:
   

   -0000000000000000000000000000111
   +00000000000000000000000000111
   

3. To fill the vacant 2 bits, zeros are inserted in the two rightmost positions:
   

   -00000000000000000000000000111
   +0000000000000000000000000011100
   

4. The result, 11100, is now converted to decimal 28 and returned.

As a general rule, applying Left shift to x by y bits returns x multiplied by the yth power of 2:

x << y = x×2^y

In our example above, this rule translates to:

7 << 2 = 7×2² = 7 × 4 = 28

>> (Sign-propagating right shift)

Sign-propagating right shift (>>) shifts bits of the first operand to the right by the number of positions defined by the second operand. Bits shifted off to the right are discarded. Bit positions that free up on the left are filled with copies of the bit that was previously leftmost.

Because the leftmost bit defines the sign of the number, the resulting sign never changes, which explains "sign-propagating" in the operator's name.

For example, 242 >> 3 returns 30:

-0000000000000000000000011110010
+0000000000000000000000000011110

>>> (Zero-fill right shift)

Similar to the previous operator, Zero-fill right shift (>>>) shifts bits of the first operand to the right by the number of positions defined by the second operand. However, vacant bit positions on the left are filled with zeros. This has two implications:

1. The result will always be positive, because a zero in the leftmost bit means a positive number.
2. For positive numbers, both right shift operators, >> and >>>, always return the same result.

For (a somewhat wild) example, -9 >>> 2 returns... 1073741821:

-11111111111111111111111111110111
+00111111111111111111111111111101

Enough with the theory though, let's discuss practice.

Is direct bit manipulation a common industry practice?

Today, you don't see bitwise operations used very often. This is because:

• Memory and CPU resources available in today's hardware make micro-optimizations with bitwise operators redundant most of the time.
• Bitwise operations aren't usually on top of an average developer's mind, which makes reading code written by others (or by yourself a month ago) harder.

That said, in some domains, bitwise operators are still in common use. These include image editing, motion graphics, data compression and encryption, device drivers, and embedded programming.

Bitwise operators can be used to create, manipulate, and read sequences of binary flags, helping save memory compared to collections of booleans. This means you sometimes see them used in error reporting and access control scenarios. For example, here's a case study describing how a combination of Bitwise OR and Bitwise AND helped check access privileges in a content management system.

Aside from these applications, you won't see bitwise operators used much. You should think twice before using them yourself unless you're sure they can bring added value in terms of improving performance or reducing complexity.

Bitwise operators in interview questions

However scarce they are in production code, bitwise operators often surface in developer interview questions. Below is a quick selection of interview questions where the expected solution involves using bitwise operators.

Swap two numbers without using an intermediate variable

One common task that can be thrown upon you in an interview is, given two variables, swap their values without introducing a third variable.

This task can be solved quickly with 3 Bitwise OR operations, using the XOR swap algorithm. Here's the sequence of these operations:

x = x ^ y;
y = x ^ y;
x = x ^ y;

Let's try to swap 2 and 5:

let x = 2 // 0010
let y = 5 // 0101

x = x ^ y; // x is now 7 (0111), y is still 5 (0101)
y = x ^ y; // x is still 7 (0111), y is now 2 (0010), 
x = x ^ y; // x becomes 5 (0101), y becomes 2 (0010)

Check if an integer is even or odd without using division

This is Bitwise AND's territory: given integer x, the expression x & 1 will return 1 if the integer is odd, and 0 if it's even. This is because all odd numbers have their rightmost bit set to 1, and 1 & 1 = 1. Here's how you check 5 for oddity:

> 0b0101 & 0b0001 // same as 5 & 1
1

For the sake or readability, you can even provide a nice wrapper around this simple operation:

const isNumberOdd = number => {
    return Boolean(number & 1);
}

Check if a positive integer is a power of 2 without branching

In binary representation of any power of (decimal) 2, one bit is set to 1, and all the following bits are set to 0:

Binary 10 = Decimal 2
Binary 100 = Decimal 4
Binary 1000 = Decimal 8
Binary 10000000000 = Decimal 1024

When we subtract 1 from any such number, we get a number where ones and zeros are inverted. For example, compare binary representations of decimal 8 and 7:

Binary 1000 = Decimal 8
Binary 0111 = Decimal 7

If we now apply Bitwise AND to these two numbers, the result will be zero. This resulting zero is what ensures we're dealing with a power of two.

(Note that you don't need to enclose number - 1 in parentheses because subtraction has a higher precedence than Bitwise AND.)

const isPowerOfTwo = number => {
    return (number & number - 1) == 0;
}

Where to learn more

Here are a few resources to check out if you want to learn more about bitwise operators, their industry usage, as well as all the crazy ways they are used and abused by geeks:

• Real world use cases of bitwise operators
• MDN JavaScript Guide: Bitwise operators
• Practical bit manipulation in JavaScript
• Twos complement: Negative numbers in binary
• The bit twiddler
• Bit Twiddling Hacks

Comments

[pentacular]

I think there are a couple of points worth mentioning.

• bitwise operations do not operate directly on the bits. They are arithmetic operations that treat numbers as compositions of powers of two. This says nothing about the underlying representation.

• bitwise operations are defined also on BigInt where the effective bit vector length is not required to be 32.