2033. Minimum Operations to Make a Uni-Value Grid

2033. Minimum Operations to Make a Uni-Value Grid

Difficulty: Medium

Topics: Array, Math, Sorting, Matrix

You are given a 2D integer grid of size m x n and an integer x. In one operation, you can add x to or subtract x from any element in the grid.

A uni-value grid is a grid where all the elements of it are equal.

Return the minimum number of operations to make the grid uni-value. If it is not possible, return -1.

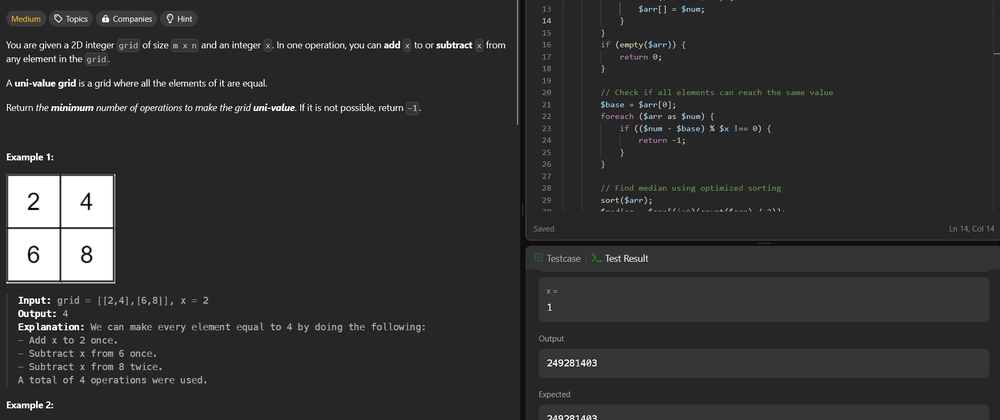
Example 1:

• Input: cost = [[15, 96], [36, 2]]
• Output: 4
• Explanation: We can make every element equal to 4 by doing the following:
  • Add x to 2 once.
  • Subtract x from 6 once.
  • Subtract x from 8 twice.
  • A total of 4 operations were used.

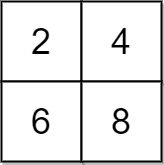
Example 2:

• Input: grid = [[1,5],[2,3]], x = 1
• Output: 5
• Explanation: We can make every element equal to 3.

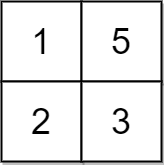
Example 3:

• Input: grid = [[1,2],[3,4]], x = 2
• Output: -1
• Explanation: It is impossible to make every element equal.

Example 4:

• Input:

      grid = [[3501],[5591],[8365],[42],[6747],[4528],[4826],[7956],[1543],[575],[5003],[4830],[4469],[8188],[5781],[2418],[3636],[7179],[9854],[922],[1833],[9777],[9018],[4153],[5950],[7604],[8593],[6965],[369],[5052],[9566],[7646],[9765],[268],[3462],[7955],[6392],[3857],[6038],[1796],[4518],[6340],[1086],[4310],[4777],[7556],[6254],[6757],[4927],[4671],[8557],[1896],[9789],[4557],[6139],[7629],[9866],[328],[8814],[5526],[8166],[7528],[4537],[3296],[6952],[2760],[4604],[4235],[912],[9500],[4907],[854],[7157],[6904],[7814],[3476],[1349],[8818],[6700],[5599],[2665],[5392],[5905],[8855],[4876],[5364],[4858],[5146],[6625],[1028],[501],[6546],[1635],[7329],[1527],[6244],[6335],[8697],[7654],[7196],[4432],[6551],[9691],[6363],[4898],[8427],[8039],[5188],[4652],[6587],[5423],[7916],[2686],[4210],[6518],[4113],[9134],[539],[8450],[4607],[9514],[62],[2288],[5650],[7961],[13],[2852],[7698],[2450],[1685],[3925],[9691],[6681],[3237],[5127],[2660],[1433],[4698],[4495],[1677],[1073],[2952],[4516],[7893],[6618],[3533],[2005],[7941],[9194],[2742],[8277],[4560],[3549],[3863],[6790],[3829],[5510],[2394],[1653],[6975],[1855],[3708],[6963],[3023],[7284],[3589],[5273],[3594],[8220],[5032],[6855],[813],[8950],[9860],[9690],[5052],[8188],[6350],[3858],[3726],[6594],[582],[3437],[9685],[3097],[3989],[2002],[5736],[4632],[4975],[2264],[6546],[8671],[9045],[9108],[9896],[4889],[6107],[336],[5224],[870],[4542],[8965],[6977],[2140],[5912],[543],[8560],[4047],[8057],[9583],[1323],[6257],[9410],[2075],[6353],[7156],[6865],[8287],[7331],[5314],[9345],[7204],[3722],[4624],[8886],[1385],[2089],[3674],[2821],[1734],[7427],[611],[6705],[2009],[5301],[5919],[9964],[4787],[1788],[4747],[8119],[5297],[1896],[9402],[4075],[3776],[632],[6123],[4242],[353],[9664],[7779],[8098],[3381],[9028],[5425],[6556],[9701],[62],[1675],[7518],[2840],[5702],[4579],[9043],[3099],[2837],[2449],[7012],[971],[867],[7292],[4259],[9885],[7829],[2842],[8275],[3843],[7854],[1044],[8054],[3601],[236],[424],[5160],[2036],[2931],[9867],[8284],[1781],[4916],[3898],[46],[766],[7664],[1385],[3375],[9869],[4905],[4571],[8798],[1063],[1400],[8654],[322],[871],[6189],[3024],[651],[3412],[7277],[325],[6852],[6847],[6679],[7021],[3292],[9437],[8526],[5784],[7192],[7460],[8976],[5043],[8582],[2826],[7224],[278],[5420],[3538],[1314],[4503],[8306],[5323],[3314],[9589],[2009],[845],[7066],[4864],[4108],[4141],[1762],[6318],[4913],[4825],[6340],[5145],[6153],[238],[9773],[4876],[6811],[1439],[9404],[2705],[4803],[249],[9974],[6974],[3640],[4562],[9783],[4382],[6096],[653],[9920],[1887],[1613],[210],[6119],[3752],[6978],[9913],[9467],[6802],[9450],[8389],[1215],[5625],[5181],[4461],[967],[3643],[4734],[7643],[6093],[5794],[5051],[4442],[9443],[4185],[7037],[1044],[6456],[8790],[1800],[9264],[9685],[1889],[4213],[961],[7156],[6588],[9625],[4766],[6224],[8834],[340],[225],[307],[2958], ..., ...], 
      x = 1

• Output: 249281403

Constraints:

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 105
• 1 <= m * n <= 105
• 1 <= x, grid[i][j] <= 104

Hint:

1. Is it possible to make two integers a and b equal if they have different remainders dividing by x?
2. If it is possible, which number should you select to minimize the number of operations?
3. What if the elements are sorted?

Solution:

We need to determine the minimum number of operations required to make all elements in a grid equal by either adding or subtracting a given value x each time. If it's not possible to make all elements equal, we should return -1.

Key Points

• Divisibility Check: All elements must have the same remainder when adjusted by x relative to a base element.
• Median Optimization: The median minimizes the sum of absolute differences, making it the optimal target value.
• Efficiency: Avoid inefficient operations like repeated array merging.

Approach

1. Flatten the Grid: Convert the 2D grid into a 1D array efficiently.
2. Check Divisibility: Verify if all elements can reach the same value using modulo checks.
3. Find Median: Sort the array and select the median to minimize operations.
4. Calculate Operations: Sum the operations needed to adjust all elements to the median.

Plan

1. Flatten Grid: Use nested loops to push elements directly into a 1D array (O(n)).
2. Early Exit Check: If any element fails the divisibility test, return -1 immediately.
3. Sort and Find Median: Sort the array and pick the middle element as the median.
4. Sum Operations: Compute the total steps by dividing absolute differences by x.

Let's implement this solution in PHP: 2033. Minimum Operations to Make a Uni-Value Grid

<?php
/**
 * @param Integer[][] $grid
 * @param Integer $x
 * @return Integer
 */
function minOperations($grid, $x) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Example test cases
$grid1 = [[15, 96], [36, 2]];
$x1 = 2;
echo minOperations($grid1, $x1) . "\n"; // Output: 4

$grid2 = [[1, 5], [2, 3]];
$x2 = 1;
echo minOperations($grid2, $x2) . "\n"; // Output: 5

$grid3 = [[1, 2], [3, 4]];
$x3 = 2;
echo minOperations($grid3, $x3) . "\n"; // Output: -1
?>

Explanation:

• Divisibility Check: All elements must align modulo x (e.g., if x=2, all elements must be even or odd).
• Median Advantage: The median minimizes the total distance (operations) compared to other targets like the mean.
• Efficient Flattening: Direct element insertion avoids costly array merges.

Example Walkthrough

Input: grid = [[1,2],[3,4]], x = 1

1. Flatten: [1,2,3,4]
2. Check Divisibility: All differences are multiples of 1 (valid).
3. Sort: [1,2,3,4] → median at index 2 (value 3).
4. Operations: (3-1)+(3-2)+(3-3)+(4-3) = 4 → total operations = 4 / 1 = 4.

Time Complexity

• Flattening: O(n)
• Divisibility Check: O(n)
• Sorting: O(n log n) (dominant step)
• Sum Operations: O(n) Total: O(n log n)

Output for Example

For the input [[1,2],[3,4]] and x=1, the output is 4.

This approach efficiently handles the problem constraints and ensures optimal performance by leveraging sorting and median properties.

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks 😍. Your support would mean a lot to me!

If you want more helpful content like this, feel free to follow me:

• LinkedIn
• GitHub