3394. Check if Grid can be Cut into Sections

3394. Check if Grid can be Cut into Sections

Difficulty: Medium

Topics: Array, Sorting

You are given an integer n representing the dimensions of an n x n grid, with the origin at the bottom-left corner of the grid. You are also given a 2D array of coordinates rectangles, where rectangles[i] is in the form [startx, starty, endx, endy], representing a rectangle on the grid. Each rectangle is defined as follows:

• (startx, starty): The bottom-left corner of the rectangle.
• (endx, endy): The top-right corner of the rectangle.

Note that the rectangles do not overlap. Your task is to determine if it is possible to make either two horizontal or two vertical cuts on the grid such that:

• Each of the three resulting sections formed by the cuts contains at least one rectangle.
• Every rectangle belongs to exactly one section.

Return true if such cuts can be made; otherwise, return false.

Example 1:

• Input: n = 5, rectangles = [[1,0,5,2],[0,2,2,4],[3,2,5,3],[0,4,4,5]]
• Output: true
• Explanation:

The grid is shown in the diagram. We can make horizontal cuts at y = 2 and y = 4. Hence, output is true.

Example 2:

• Input: n = 4, rectangles = [[0,0,1,1],[2,0,3,4],[0,2,2,3],[3,0,4,3]]
• Output: true
• Explanation:

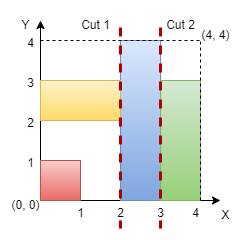
We can make vertical cuts at x = 2 and x = 3. Hence, output is true.

Example 3:

• Input: n = 4, rectangles = [[0,2,2,4],[1,0,3,2],[2,2,3,4],[3,0,4,2],[3,2,4,4]]
• Output: false
• Explanation: We cannot make two horizontal or two vertical cuts that satisfy the conditions. Hence, output is false.

Constraints:

• 3 <= n <= 109
• 3 <= rectangles.length <= 105
• 0 <= rectangles[i][0] < rectangles[i][2] <= n
• 0 <= rectangles[i][1] < rectangles[i][3] <= n
• No two rectangles overlap.

Hint:

1. For each rectangle, consider ranges [start_x, end_x] and [start_y, end_y] separately.
2. For x and y directions, check whether we can split it into 3 parts.

Solution:

We need to determine if we can make two horizontal or vertical cuts on an n x n grid such that the grid is divided into three sections, each containing at least one rectangle without any overlap. The approach involves checking both horizontal and vertical directions to see if such cuts are possible.

Approach

1. Collect Intervals: For each rectangle, collect the x and y intervals.
2. Merge Intervals: For each direction (x and y), merge overlapping intervals to form non-overlapping contiguous intervals.
3. Check Validity: If the number of merged intervals in either direction is at least three, then it is possible to make the required cuts. This is because three or more non-overlapping intervals can be split into three sections with two cuts.

Let's implement this solution in PHP: 3394. Check if Grid can be Cut into Sections

<?php
/**
 * @param Integer $n
 * @param Integer[][] $rectangles
 * @return Boolean
 */
function checkValidCuts($n, $rectangles) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

/**
 * @param $intervals
 * @return int
 */
private function countMerged($intervals) {
    ...
    ...
    ...
    /**
     * go to ./solution.php
     */
}

// Example Test Cases
$n1 = 5;
$rectangles1 = [[1,0,5,2],[0,2,2,4],[3,2,5,3],[0,4,4,5]];
echo checkValidCuts($n1, $rectangles1) ? 'true' : 'false'; // Output: true

$n2 = 4;
$rectangles2 = [[0,0,1,1],[2,0,3,4],[0,2,2,3],[3,0,4,3]];
echo "\n" . (checkValidCuts($n2, $rectangles2) ? 'true' : 'false'); // Output: true

$n3 = 4;
$rectangles3 = [[0,2,2,4],[1,0,3,2],[2,2,3,4],[3,0,4,2],[3,2,4,4]];
echo "\n" . (checkValidCuts($n3, $rectangles3) ? 'true' : 'false'); // Output: false
?>

Explanation:

1. Collect Intervals: For each rectangle, extract the x and y intervals. Each interval is represented as a pair of start and end points.
2. Merge Intervals: Sort the intervals by their start points. Then, merge overlapping or adjacent intervals to form non-overlapping contiguous intervals. The merging process ensures that we can check for the minimum number of contiguous sections.
3. Check Validity: After merging, if the number of non-overlapping intervals in either the x or y direction is at least three, then it is possible to make two cuts to divide the grid into three sections. Each section will contain at least one merged interval, ensuring that each section has at least one rectangle.

This approach efficiently checks both directions and leverages interval merging to determine the feasibility of the required cuts. The solution runs in O(n log n) time due to sorting and merging intervals, which is efficient given the problem constraints.

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks 😍. Your support would mean a lot to me!

If you want more helpful content like this, feel free to follow me:

• LinkedIn
• GitHub