LeetCode Meditations: Subtree of Another Tree

Let's start with the description for this one:

Given the roots of two binary trees root and subRoot, return true if there is a subtree of root with the same structure and node values of subRoot and false otherwise.

A subtree of a binary tree tree is a tree that consists of a node in tree and all of this node's descendants. The tree tree could also be considered as a subtree of itself.

For example:

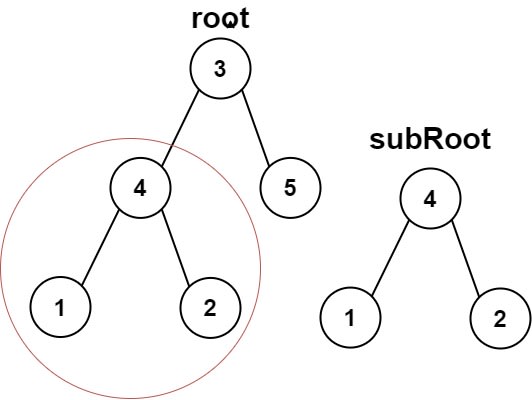
Input: root = [3, 4, 5, 1, 2], subRoot = [4, 1, 2]
Output: true

Or:

Input: root = [3, 4, 5, 1, 2, null, null, null, null, 0], subRoot = [4, 1, 2]
Output: false

---

When it comes to tree problems (at least the ones we've looked at so far), recursion seems to be a natural choice, as trees themselves are recursive structures. And this problem is no different.

What we need to do is check whether a subtree of the first tree we're given is the same as another tree.
In the previous problem, we did just that: we've checked if two trees are the same.

So, we can use the same function here as well. Here's a concise isSameTree function:

function isSameTree(p: TreeNode | null, q: TreeNode | null): boolean {
  if (p === null && q === null) {
    return true;
  } 

  if (p !== null && q !== null && p.val === q.val) {
    return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
  } else {
    return false;
  }
}

Now for this problem, we need to check if, with the given root and subRoot, the trees are the same. If not, we need to recursively search left and right subtrees for sameness.

However, coming up with edge cases was harder than I thought. For one thing, we don't want to check the case when both root and subRoot are null — they need to be handled separately. NeetCode's explanation was very helpful to sort this out in my mind.

So, we can check the case when the subRoot is null, in that case we can return true because an empty tree is a subtree of every tree.
However, when the root is null and the subRoot is not null, we need to return false, because that means the given subtree is not in the tree.

When the current root and subRoot are holding the same tree, we can return true, but in other cases, we recursively search the left and right subtrees until they result in the same tree or the root ends up being null:

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *   val: number
 *   left: TreeNode | null
 *   right: TreeNode | null
 *   constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *     this.val = (val === undefined ? 0 : val)
 *     this.left = (left === undefined ? null : left)
 *     this.right = (right === undefined ? null : right)
 *   }
 * }
 */

function isSubtree(root: TreeNode | null, subRoot: TreeNode | null): boolean {
  // The order of these two base cases is important!
  if (subRoot === null) {
    return true;
  }

  if (root === null) { // (root === null && subRoot !== null)
    return false;
  }

  if (isSameTree(root, subRoot)) {
    return true;
  } else {
    return isSubtree(root.left, subRoot) || isSubtree(root.right, subRoot);
  }
}

Note
The order of the first two base cases is important. The second one where we check if root is null implicitly assumes that subRoot is not null as we have checked that condition in the first if statement.

Time and space complexity

For each node in the first tree, we use the isSameTree function to check if the tree is the same as the given subtree. Therefore the time complexity is in the worst case $O(n^2)$ .
Because of the recursive calls, the space complexity is—I think—in the worst case $O(n)$ .

---

Next up is Lowest Common Ancestor of a Binary Search Tree. That's a mouthful, but we'll manage.
Until then, happy coding.