LeetCode Meditations: Word Search

The description for Word Search is:

Given an m x n grid of characters board and a string word, return true if word exists in the grid.

The word can be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once.

For example:

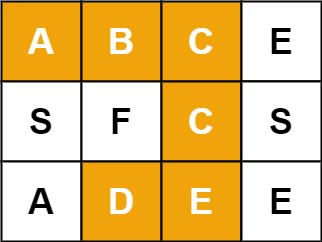
Input: board = [['A', 'B', 'C', 'E'], ['S', 'F', 'C', 'S'], ['A', 'D', 'E', 'E']], word = 'ABCCED'

Output: true

---

We somehow have to look at each cell, and explore our options to see if we can find the word. This exploration lends itself perfectly to a depth-first search.

But, we can't explore other cells if the current row and column we're looking at are out of bounds, and the current character is not the character we want.

In these cases, we have to return false:

if (outOfBounds(row, col) || word[idx] !== board[row][col]) {
  return false;
}

Note
idx is the index of the current character in word that we're looking for.

This is one base case. Another base case is when we actually find the word.

Since we'll be keeping track of the index of the word for the current character we're exploring, once it reaches the word's length, we know that we have found the word:

if (idx === word.length) {
  return true;
}

Now that the base cases are out of the way, the first thing we can do for the cell we're looking at is to mark it as visited. We can use the * character to indicate that:

let currentCell = board[row][col];
board[row][col] = '*'; 

Now, we can do the exploring for the cell we're looking at:

dfs(row + 1, col, idx + 1) || // down
dfs(row - 1, col, idx + 1) || // up
dfs(row, col + 1, idx + 1) || // right
dfs(row, col - 1, idx + 1);   // left

Note
We'll pass idx + 1 as our new index, because we'll be looking for the next character in word.

All these explorations are not for nothing of course, so we have to keep the result we have:

let result = dfs(row + 1, col, idx + 1) || // down
             dfs(row - 1, col, idx + 1) || // up
             dfs(row, col + 1, idx + 1) || // right
             dfs(row, col - 1, idx + 1);   // left

Before returning this result, we need to reset the marked cell to its original value, otherwise, in our other explorations, we would have it wrongly marked:

board[row][col] = currentCell;

This is all for our depth-first search function:

function dfs(row: number, col: number, idx: number): boolean {
  if (idx === word.length) {
    return true;
  }
  if (outOfBounds(row, col) || word[idx] !== board[row][col]) {
    return false;
  }

  // Mark the current cell as visited
  let currentCell = board[row][col];
  board[row][col] = '*'; 

  // Pass idx + 1 because we're looking for 
  // the next character in the word now
  let result = dfs(row + 1, col, idx + 1) || // down
               dfs(row - 1, col, idx + 1) || // up
               dfs(row, col + 1, idx + 1) || // right
               dfs(row, col - 1, idx + 1);   // left

  // Reset the current cell to its original value 
  // because we're done visiting it
  board[row][col] = currentCell;

  return result;
}

We'll apply depth-first search for each cell on the board:

for (let i = 0; i < rowsLength; i++) {
  for (let j = 0; j < colsLength; j++) {
    if (dfs(i, j, 0)) {
      return true;
    }
  }
}

If dfs returns true for that cell, we can return true immediately. Otherwise, we'll return false at the end.

The final solution looks like this in TypeScript:

function exist(board: string[][], word: string): boolean {
  const rowsLength = board.length;
  const colsLength = board[0].length;

  function outOfBounds(r: number, c: number) {
    return r < 0 || c < 0 || r >= rowsLength || c >= colsLength;
  }

  // idx: the index of the current character in the word we're looking for
  function dfs(row: number, col: number, idx: number): boolean {
    if (idx === word.length) {
      return true;
    }
    if (outOfBounds(row, col) || word[idx] !== board[row][col]) {
      return false;
    }

    // Mark the current cell as visited
    let currentCell = board[row][col];
    board[row][col] = '*'; 

    // Pass idx + 1 because we're looking for 
    // the next character in the word now
    let result = dfs(row + 1, col, idx + 1) || // down
                 dfs(row - 1, col, idx + 1) || // up
                 dfs(row, col + 1, idx + 1) || // right
                 dfs(row, col - 1, idx + 1);   // left

    // Reset the current cell to its original value 
    // because we're done visiting it
    board[row][col] = currentCell;

    return result;
  }

  // For each cell, do a depth-first search
  for (let i = 0; i < rowsLength; i++) {
    for (let j = 0; j < colsLength; j++) {
      if (dfs(i, j, 0)) {
        return true;
      }
    }
  }

  return false;
}

This version is adapted from NeetCode's solution.

---

Now, let's look at a very simple example.

Our board looks like this, and the word we're looking for is PIE:

board = [['A', 'P'], ['E', 'I']]

word = 'PIE'

Let's modify the code a little bit, and use some helpful console.logs:

function exist(board: string[][], word: string): boolean {
  const rowsLength = board.length;
  const colsLength = board[0].length;

  function outOfBounds(r: number, c: number) {
    return r < 0 || c < 0 || r >= rowsLength || c >= colsLength;
  }

  // idx: the index of the current character in the word we're looking for
  function dfs(row: number, col: number, idx: number): boolean {
    console.log(`\n===== row: ${row}, col: ${col} =====`);
    if (idx === word.length) {
      console.log(`🎉 this is dfs(${row}, ${col}, ${idx}), FINISHED ALREADY, '${word}' HAS BEEN FOUND`);
      return true;
    }
    if (outOfBounds(row, col)) {
      console.log(`\n======= OUT OF BOUNDS =======\n`);
      return false;
    }
    if (word[idx] !== board[row][col]) {
      console.log(`looking for '${word[idx]}', this is ${board[row][col]}`);
      return false;
    }

    // Mark the current cell as visited
    let currentCell = board[row][col];
    console.log(`found ${currentCell}, currentCell is ${currentCell}, idx is ${idx}`);
    board[row][col] = '*'; 

    // Pass idx + 1 because we're looking for 
    // the next character in the word now
    console.log(`this is dfs(${row}, ${col}, ${idx}), going down, searching for '${word[idx + 1]}'`); 
    let downResult = dfs(row + 1, col, idx + 1); 
    console.log(`🟣 dfs(${row + 1}, ${col}, ${idx + 1}) returned, row is ${row}, col is ${col}\n`);

    console.log(`this is dfs(${row}, ${col}, ${idx}), going up, searching for '${word[idx + 1]}'`);
    let upResult = dfs(row - 1, col, idx + 1);
    console.log(`🟣 dfs(${row - 1}, ${col}, ${idx + 1}) returned, row is ${row}, col is ${col}\n`);

    console.log(`this is dfs(${row}, ${col}, ${idx}), going right, searching for '${word[idx + 1]}'`);
    let rightResult = dfs(row, col + 1, idx + 1);
    console.log(`🟣 dfs(${row}, ${col + 1}, ${idx + 1}) returned, row is ${row}, col is ${col}\n`);

    console.log(`this is dfs(${row}, ${col}, ${idx}), going left, searching for '${word[idx + 1]}'`);
    let leftResult = dfs(row, col - 1, idx + 1);
    console.log(`🟣 dfs(${row}, ${col - 1}, ${idx + 1}) returned, row is ${row}, col is ${col}\n`);

    // Reset the current cell to its original value 
    // because we're done visiting it
    board[row][col] = currentCell;

    return downResult || upResult || rightResult || leftResult;
  }

  // For each cell, do a depth-first search
  for (let i = 0; i < rowsLength; i++) {
    for (let j = 0; j < colsLength; j++) {
      if (dfs(i, j, 0)) {
        return true;
      }
    }
  }

  return false;
}

console.log(exist([['A', 'P'],['E', 'I']], 'PIE'));

It looks overwhelming and cluttered, but looking at the output, it almost reads like a story:

===== row: 0, col: 0 =====
looking for 'P', this is A

===== row: 0, col: 1 =====
found P, currentCell is P, idx is 0
this is dfs(0, 1, 0), going down, searching for 'I'

===== row: 1, col: 1 =====
found I, currentCell is I, idx is 1
this is dfs(1, 1, 1), going down, searching for 'E'

===== row: 2, col: 1 =====

======= OUT OF BOUNDS =======

🟣 dfs(2, 1, 2) returned, row is 1, col is 1

this is dfs(1, 1, 1), going up, searching for 'E'

===== row: 0, col: 1 =====
looking for 'E', this is *
🟣 dfs(0, 1, 2) returned, row is 1, col is 1

this is dfs(1, 1, 1), going right, searching for 'E'

===== row: 1, col: 2 =====

======= OUT OF BOUNDS =======

🟣 dfs(1, 2, 2) returned, row is 1, col is 1

this is dfs(1, 1, 1), going left, searching for 'E'

===== row: 1, col: 0 =====
found E, currentCell is E, idx is 2
this is dfs(1, 0, 2), going down, searching for 'undefined'

===== row: 2, col: 0 =====
🎉 this is dfs(2, 0, 3), FINISHED ALREADY, 'PIE' HAS BEEN FOUND
🟣 dfs(2, 0, 3) returned, row is 1, col is 0

this is dfs(1, 0, 2), going up, searching for 'undefined'

===== row: 0, col: 0 =====
🎉 this is dfs(0, 0, 3), FINISHED ALREADY, 'PIE' HAS BEEN FOUND
🟣 dfs(0, 0, 3) returned, row is 1, col is 0

this is dfs(1, 0, 2), going right, searching for 'undefined'

===== row: 1, col: 1 =====
🎉 this is dfs(1, 1, 3), FINISHED ALREADY, 'PIE' HAS BEEN FOUND
🟣 dfs(1, 1, 3) returned, row is 1, col is 0

this is dfs(1, 0, 2), going left, searching for 'undefined'

===== row: 1, col: -1 =====
🎉 this is dfs(1, -1, 3), FINISHED ALREADY, 'PIE' HAS BEEN FOUND
🟣 dfs(1, -1, 3) returned, row is 1, col is 0

🟣 dfs(1, 0, 2) returned, row is 1, col is 1

🟣 dfs(1, 1, 1) returned, row is 0, col is 1

this is dfs(0, 1, 0), going up, searching for 'I'

===== row: -1, col: 1 =====

======= OUT OF BOUNDS =======

🟣 dfs(-1, 1, 1) returned, row is 0, col is 1

this is dfs(0, 1, 0), going right, searching for 'I'

===== row: 0, col: 2 =====

======= OUT OF BOUNDS =======

🟣 dfs(0, 2, 1) returned, row is 0, col is 1

this is dfs(0, 1, 0), going left, searching for 'I'

===== row: 0, col: 0 =====
looking for 'I', this is A
🟣 dfs(0, 0, 1) returned, row is 0, col is 1

true

There are several insights here — for example, note that this line:

this is dfs(1, 0, 2), going down, searching for 'undefined'

indicates that we still go looking for word[idx + 1] even though the current index is the index of the last character in word.

It, of course, continues exploring every direction left from there on:

this is dfs(1, 0, 2), going up, searching for 'undefined'

this is dfs(1, 0, 2), going right, searching for 'undefined'

this is dfs(1, 0, 2), going left, searching for 'undefined'

Again, also these lines:

this is dfs(0, 1, 0), going up, searching for 'I'

this is dfs(0, 1, 0), going right, searching for 'I'

this is dfs(0, 1, 0), going left, searching for 'I'

indicate that once the control returns to the function that has found 'P', it'll still continue exploring all the directions left from there. We've already found 'PIE' by going down, but the other directions are still being explored.

Time and space complexity

The time complexity will be

$$O(\text{ length of rows } * \text{ length of columns } * 4^{\text{ length of the word }})$$

We can denote it succinctly as $O(n * m * 4^l)$ where $n$ is the length of rows, $m$ is the length of columns, and $l$ is the length of the word. The reason is that we call dfs for each cell on the board ( $n * m$ ), and there can be $4^l$ recursive calls to dfs.

The space complexity is going to be $O(l)$ where $l$ is the length of the word, as the stack depth can reach $l$ in the worst case.

---

Backtracking might not be very efficient or elegant, and it's definitely a brute force solution for a given problem. Now that we're done with this chapter, we can take a deep breath.

Next up, we'll take a look at the trie data structure. Until then, happy coding.