Solution: Short Encoding of Words (ver. 2)

This is part of a series of Leetcode solution explanations (index). If you liked this solution or found it useful, please like this post and/or upvote my solution post on Leetcode's forums.

---

Note: This is my second version of a solution for this problem. Due to the constraints listed for this problem, the first version is the more performant solution, but the nature of this problem really calls for a trie solution, so I've included a breakdown of the trie approach here, as well.

---

Leetcode Problem #820 (Medium): Short Encoding of Words

---

Description:

(Jump to: Solution Idea || Code: JavaScript | Python | Java | C++)

A valid encoding of an array of words is any reference string s and array of indices indices such that:

• words.length == indices.length
• The reference string s ends with the '#' character.
• For each index indices[i], the substring of s starting from indices[i] and up to (but not including) the next '#' character is equal to words[i].

Given an array of words, return the length of the shortest reference string s possible of any valid encoding of words.

---

Examples:

Example 1:
Input:	words = ["time", "me", "bell"]
Output:	10
Explanation:	A valid encoding would be s = "time#bell#" and indices = [0, 2, 5]. words[0] = "time", the substring of s starting from indices[0] = 0 to the next '#' is underlined in "time#bell#" words[1] = "me", the substring of s starting from indices[1] = 2 to the next '#' is underlined in "time#bell#" words[2] = "bell", the substring of s starting from indices[2] = 5 to the next '#' is underlined in "time#bell#"

Example 2:
Input:	words = ["t"]
Output:	2
Explanation:	A valid encoding would be s = "t#" and indices = [0].

---

Constraints:

• 1 <= words.length <= 2000
• 1 <= words[i].length <= 7
• words[i] consists of only lowercase letters.

---

Idea:

(Jump to: Problem Description || Code: JavaScript | Python | Java | C++)

So a simple encoding of the input would be to add the '#' marker to the end of each word and then join them in a string. Per the instructions, this encoding can be made shorter if you can combine two or more words into one encoded word. In order to do this, the smaller word would have to be not just a substring of the larger word, but the rightmost substring, or its suffix.

A naive solution here would be to compare each word to each other word and examine if the larger word has the smaller word as its suffix, but with a range of up to 2000 words, that would mean almost 4 million potential combinations.

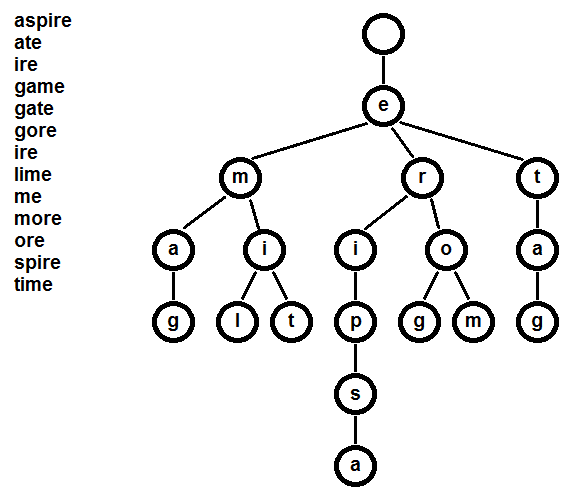
But if we're asked to check for matching suffixes, we might also be thinking of a trie solution. A trie is a tree data structure in which you define branches of prefix (or in this case suffix) data. In this way, entries that share the same prefix will be grouped together and easy to identify.

When you build out a trie, you iterate through the granular segments of the data and go down existing branches of the trie when they exist and create them when they don't. For this problem, the entries are words and thus the granular segments are characters. We'll also be iterating through the characters in reverse order, since we're dealing with suffixes instead of prefixes.

We could fully build out the trie then later traverse the trie to calculate our answer (ans), but instead we can just keep our ans up-to-date as we build out the trie to be more efficient.

As we build out our trie, there are three things we have to look out for:

• If any new branches are formed while processing a word, then that word must be new and we should add its length (plus 1 for the '#' at the end) to our ans.
• If a word ends without forging a new branch, then it must be the suffix of an earlier word, so we shouldn't add its length to our ans.
• If there are no other branches on the node in which the first new branch is formed while processing a word, then some earlier word must be a suffix to the current word, so we should subtract the already added amount from our ans.

The third check in particular will allow us to avoid needing to sort W before entry. In order to prevent the third check from triggering every time a word extends into new territory (which would happen with each new character), we can use a boolean flag (newWord) to mark only the first instance.

---

Implementation:

Javascript and Python are a little more straightforward in their implementation of the trie. They can use a more simple map structure to good use.

For Java and C++, however, we'll want to use a class structure for our trie, but rather than use data structures with more overhead, we can improve efficiency by simplifying each node to an array of 26 elements, with each index corresponding to a character.

The one additional problem we face when converting from a map-type object to an ordered array is that we no longer have an easy way to tell whether or not the array is fully empty. To get around this, we can just add an isEmpty boolean flag to our TrieNode class.

---

Javascript Code:

(Jump to: Problem Description || Solution Idea)

var minimumLengthEncoding = function(W) {
    let len = W.length, trie = new Map(), ans = 1
    for (let word of W) {
        let curr = trie, newWord = false
        for (let j = word.length - 1; ~j; j--) {
            let char = word.charAt(j)
            if (!curr.size && !newWord)
                ans -= word.length - j
            if (!curr.has(char))
                newWord = true, curr.set(char, new Map())
            curr = curr.get(char)
        }
        if (newWord) ans += word.length + 1
    }
    return ans
};

---

Python Code:

(Jump to: Problem Description || Solution Idea)

class Solution:
    def minimumLengthEncoding(self, W: List[str]) -> int:
        trie, ans = defaultdict(), 1
        for word in W:
            curr, newWord = trie, False
            for i in range(len(word)-1,-1,-1):
                char = word[i]
                if not curr and not newWord: ans -= len(word) - i
                if char not in curr:
                    newWord = True
                    curr[char] = defaultdict()
                curr = curr[char]
            if newWord: ans += len(word) + 1
        return ans

---

Java Code:

(Jump to: Problem Description || Solution Idea)

class TrieNode {
    TrieNode[] branch = new TrieNode[26];
    Boolean isEmpty = true;
}

class Solution {
    public int minimumLengthEncoding(String[] W) {
        TrieNode trie = new TrieNode();
        trie.branch = new TrieNode[26];
        int ans = 1;
        for (String word : W) {
            TrieNode curr = trie;
            Boolean newWord = false;
            for (int i = word.length() - 1; i >= 0; i--) {
                int c = word.charAt(i) - 'a';
                if (curr.isEmpty && !newWord) ans -= word.length() - i;
                if (curr.branch[c] == null) {
                    curr.branch[c] = new TrieNode();
                    newWord = true;
                    curr.isEmpty = false;
                }
                curr = curr.branch[c];
            }
            if (newWord) ans += word.length() + 1;
        }
        return ans;
    }
}

---

C++ Code:

(Jump to: Problem Description || Solution Idea)

struct TrieNode {
    TrieNode *branch[26];
    bool isEmpty = true;
};

class Solution {
public:
    int minimumLengthEncoding(vector<string>& W) {
        TrieNode *trie = new TrieNode();
        int ans = 1;
        for (string word : W) {
            TrieNode *curr = trie;
            bool newWord = false;
            for (int i = word.size() - 1; i >= 0; i--) {
                int c = word[i] - 97;
                if (curr->isEmpty && !newWord) ans -= word.size() - i;
                if (!curr->branch[c]) {
                    newWord = true;
                    curr->branch[c] = new TrieNode();
                    curr->isEmpty = false;
                }
                curr = curr->branch[c];
            }
            if (newWord) ans += word.size() + 1;
        }
        return ans;
    }
};