Detecting Graph Cycles With Depth-First Search

Resources:

1. Video on detecting cycles in directed graphs
2. Video on detecting cycles in undirected graphs
3. MIT video on detecting cycles in graphs
4. Helpful implementation for detecting cycles in adjacency matrix
5. Deadlock Detection in the book: Elements of Programming Interviews

To get the most out of this article, it is helpful if you already know what a graph is, and ideally what depth-first search is. A previous post of mine covers the basics of graphs and graph traversals.

Some takeaways:

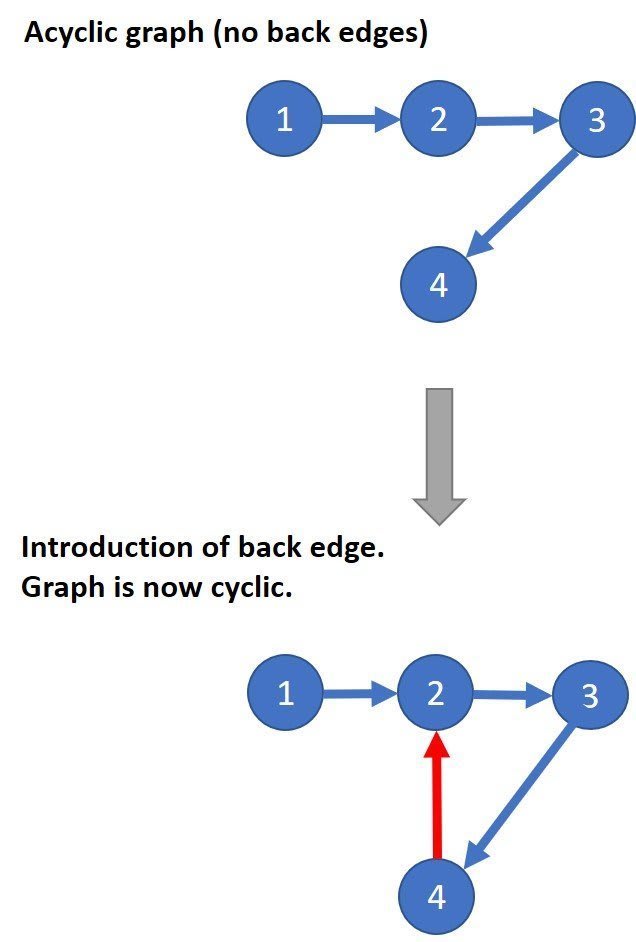
• A graph cycle is when there is a "loop" or circular reference. This can be a series of edges that connect back to an origin vertex.
• If a graph has a cycle it is a cyclic graph.
• To determine if a graph has a cycle, we can traverse the graph and look for a back edge.
  • A back edge is one that connects a vertex to an already visited ancestor.
  • Example:

• To detect a cycle in a directed graph (i.e to find a back edge), you can use depth-first search (with some introduction of local state to tell you if a back edge occurs):
  • We will maintain 3 buckets of vertices: white, grey, & black buckets. (We can also colour vertices instead).
    • The white bucket will contain all of the unvisited vertices. At the start of our traversal, this means every vertex is in the white bucket.
    • Before visiting a vertex, we will move it from the white bucket into the grey bucket.
    • After fully visiting a vertex, it will get moved from the grey bucket into the black bucket.
    • We can skip over vertices already in the black bucket, if we happen to try and visit them again.
    • When visiting the children/descendants of a vertex, if we come to a descendant vertex that is already in the grey bucket - that means we have found a back edge/cycle.
    • This means the current vertex has a back edge to it's ancestor - as we only arrived at the current vertex via it's ancestor. So we have just determined that there is more than one path between the two (a cycle).
• To detect a cycle in an undirected graph, it is very similar to the approach for a directed graph. However, there are some key differences:
  • We no longer colour vertices/maintain buckets.
  • We have to make sure to account for the fact that edges are bidirectional - so an edge to an ancestor is allowed, if that ancestor is the parent vertex.
  • We only keep track of visited vertices (similar to the grey bucket).
  • When exploring/visiting all descendants of a vertex, if we come across a vertex that has already been visited then we have detected a cycle.
• Time complexity is O(v + e) for an adjacency list. Space complexity is O(v). For an adjacency matrix, the time & space complexity would be O(v^2).

Although using depth-first search is common for cycle detection, you can also detect cycles using topological sort too. I have yet to cover topological sorting of graphs - but will be doing so in a later post.

Below are implementations of cycle detection via depth-first search in both undirected & directed graphs. I have implemented each for an adjacency list (Graph) & an adjacency matrix (Graph2):

As always, if you found any errors in this post please let me know!