Advent of Code 2018 Day 3
Try the simulator for Part 1 using your puzzle input!
Task: Solve for X where...
Part 1
X = the number of square inches of fabric that are within two or more claims
Part 2
X = the ID of the only claim that doesn't overlap
Example input
#1 @ 1,3: 4x4
#2 @ 3,1: 4x4
#3 @ 5,5: 2x2
It represents:
- A series of claims, one from each Elf
Each claim:
- Has a unique ID
- Defines a single rectangle
- Defines that rectangle's size
- Defines that rectangle's location relative to the top-left edge of a larger piece of fabric
Part 1
- Determining the smallest possible dimensions of the fabric
- Rendering each claim in the fabric
- Counting the overlapped square inches
Determining the smallest possible dimensions of the fabric
The instructions offer a single claim as an initial example:
#123 @ 3,2: 5x4
- ID is 123
- 3 inches from the left edge of the fabric
- 2 inches from the top edge of the fabric
- 5 inches wide
- 4 inches tall
An illustration is also offered:
...........
...........
...#####...
...#####...
...#####...
...#####...
...........
...........
...........
However, my algorithm should only concern itself with the smallest necessary size of fabric.
That would crop the illustration to this:
........
........
...#####
...#####
...#####
...#####
This fabric size is 8x6.
How might I have programmatically calculated those dimensions using the claim?
#123 @ 3,2: 5x4
X,Y XxY
X + X = 8
Y + Y = 6
It worked with one claim. Now to try with several.
The other example offered is this:
#1 @ 1,3: 4x4
#2 @ 3,1: 4x4
#3 @ 5,5: 2x2
The search for the fabric's smallest possible dimensions goes like this:
dimensions = 0x0
#1 @ 1,3: 4x4
1 + 4 = 5 (new max!)
3 + 4 = 7 (new max!)
dimensions = 5x7
#2 @ 3,1: 4x4
3 + 4 = 7 (new max!)
1 + 4 = 5
dimensions = 7x7
#3 @ 5,5: 2x2
5 + 2 = 7
5 + 2 = 7
dimensions unchanged
The illustration depicts:
........
...2222.
...2222.
.11XX22.
.11XX22.
.111133.
.111133.
........
And when cropped to the smallest possible dimensions:
.......
...2222
...2222
.11XX22
.11XX22
.111133
.111133
Which is 7x7!
It seems like I have - in theory - a working algorithm for identifying the smallest possible dimensions of my fabric.
Now I need to write it.
...
I wrote it!
My puzzle input's fabric dimensions appear to be:
1000x999
That concerns me, because the instructions state:
The whole piece of fabric they're working on is a very large square - at least 1000 inches on each side.
- Am I miscalculating my fabric's height?
- I might be
- But I want to move on to rendering each claim in the fabric
Rendering each claim in the fabric
- I need a 2D array
- I'll set each cell initially to
. - I'll update the cells being painted for the first time with a
| - I'll update the cells being painted after the first time with a
#
By now, writing that algorithm felt natural.
I saw what I expected for both the sample and example inputs:
#123 @ 3,2: 5x4
........
........
...|||||
...|||||
...|||||
...|||||
#1 @ 1,3: 4x4
#2 @ 3,1: 4x4
#3 @ 5,5: 2x2
.......
...||||
...||||
.||##||
.||##||
.||||||
.||||||
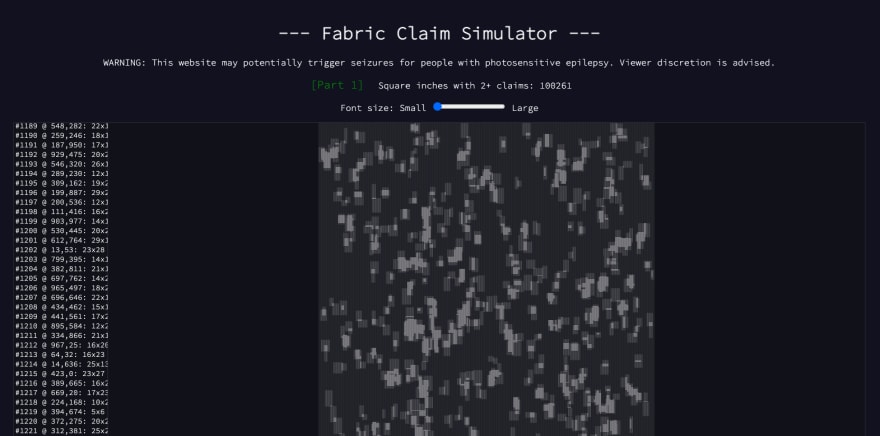
Now I need to build a simulator so I can see the 1000x999-inch fabric with each claim rendered.
...
In almost no time at all, I saw my fabric:

It seemed comprehensive, with two claims touching the right- and bottom-most sides.
Counting the overlapped square inches
This was a simple process of reduction:
For each row of fabric
Count the number of cells containing a #
Return the sum
Testing the results:
- It worked with the example input!
- It worked with my puzzle input!
Part 2
- Thank goodness for my simulator!
- Finding the claim's ID
Thank goodness for my simulator!
- I need to find the one claim that doesn't overlap.
- I spent a few minutes scanning my fabric as generated by my simulator.
- I nearly gave up, when suddenly I spotted the obvious contender
Zooming out to show it within the full piece of fabric:

Finding the claim's ID
- I see the claim
- What's one quick way to get its ID?
- Use my browser's console!
What I did:
- Highlight all the characters up to - but not including - the top-left corner of the claim
- Copy-paste them as a string into the browser console
- Get the length of the string
- Use
find()to search my list of claims for the array whose second element equaled the length...hoping it found one, and only one - Copy-pasting the first element's value into the answer box
- Smile with glee that I earned two gold stars!
I did it!!
- I solved both parts!
- I made a simulator that enabled me to solve Part 2!
Bummer:
- I'm not sure how I would have solved Part 2 without seeing the fabric
- It would make for a fun puzzle to come back to one day





Top comments (0)