Advent of Code 2019 Day 10
Task: Solve for X where...
Part 1
X = the number of visible asteroids that can be detected from the asteroid where the most asteroids are visible
Part 2
X = the result of an equation leveraging the coordinates of the 200th asteroid destroyed by a laser located on the asteroid identified in Part 1
Example input
.#..#
.....
#####
....#
...##
It represents:
- A map of all the asteroids in a region of space
-
.s are emptiness -
#s are asteroids (tiny ones that only occupy a small space at the center of that location)
Part 1
- Visualizing each angle for a few points to try crafting an algorithm
- Considering better paths that an algorithm could follow
- A visual depiction of the algorithm I plan to build
- A written summary of how the algorithm should work
- Woah. That worked! I'm shocked!
Visualizing each angle for a few points to try crafting an algorithm
Here's the example input again:
.#..#
.....
#####
....#
...##
I'll use the center asteroid in the example input map region:
#
The eight easy lines of sight to check are horizontal, vertical and diagonals:
\ | /
812
-7#3-
654
/ | \
Using center as (0,0):
- 1 is at angle (-1, 0)
- 2 is at angle (-1, 1)
- 3 is at angle ( 0, 1)
- 4 is at angle ( 1, 1)
- 5 is at angle ( 1, 0)
- 6 is at angle ( 1,-1)
- 7 is at angle ( 0,-1)
- 8 is at angle (-1,-1)
But how would I get each of the other 352 angles?
Or, well, other 8 angles in this example?
8 1
7 2
#
6 3
5 4
Using center as (0,0):
- 1 is at angle (-2, 1)
- 2 is at angle (-1, 2)
- 3 is at angle ( 1, 2)
- 4 is at angle ( 2, 1)
- 5 is at angle ( 2,-1)
- 6 is at angle ( 1,-2)
- 7 is at angle (-1,-2)
- 8 is at angle (-2,-1)
Do I notice any patterns?
- The range for X,Y values spans the boundaries of the region: from (0,0) it's (-2 to 2, -2 to 2)
Here's the example input again:
.#..#
.....
#####
....#
...##
Now, I'll use the winning asteroid in the example input map region:
.....
.....
.....
.....
...#.
The direct lines to check are:
First angle: (-1,0) until an asteroid is spotted or the region boundary is exceeded
- Check (-1,0): empty
- Check (-2,0): hit! stop
Next angle: (-4,1)...
- Check (-4,1): hit! stop
Next angle: (-3,1)...
- Check (-3,1): empty
- Check (-6,2): out of range! stop
Next angle: (-2,1)...
- Check (-2,1): hit! stop
Next angle: (-1,1)...
- Check (-1,1): hit! stop
Next angle: ( 0,1)...
- Check (0,1): hit! stop
Somehow skip to degrees 90 - 269.
Next angle: (0,-1)...
- Check (0,-1): empty
- Check (0,-2): empty
- Check (0,-3): empty
- Check (0,-4): out of range! stop
Next angle: (-1, -3)...
- Check (-1, -3): empty
- Check (-2, -6): out of range! stop
Next angle: (-1, -2)...
- Check (-1, -2): empty
- Check (-2, -4): out of range! stop
Next angle: (-1, -1)...
- Check (-1, -1): empty
- Check (-2, -2): hit! stop
Next angle: (-2, -1)...
- Check (-2, -1): hit! stop
Next angle: (-3, -1)...
- Check (-3, -1): empty
- Check (-6, -2): out of range! stop
Next angle: (-4, -1)...
- Check (-4, -1): empty
- Check (-8, -2): out of range! stop
Wait, that's only 7 hits. There should be 8. What did I miss?
.....
.....
*....
.....
...S.
That is at angle: (-2, -3)
How could I have targeted that?
- Not via any (-1,x) path
- Only via the (-2,x) path
But from (-2,-1) there's:
- (-2,-2), which has already been checked
I guess I could have just kept going until out of range:
- (-2,-3): hasn't been checked, is a hit!
So, what might my path have been?
Part 1
....3
....4
...25
...16
...#7
Part 2
....x
....x
.7.xx
456xx
321#x
Part 3
987.x
654.x
321xx
xxxxx
xxx#x
That seems like a custom path, not one followed by some consistently incrementing or decrementing X,Y relative coordinates.
Considering better paths that an algorithm could follow
The example input, again:
.#..#
.....
#####
....#
...##
From the middle point, four paths that start from each diagonal and continue toward a border:
^^ ->
|| ->
#
<- ||
<- vv
Followed by checks of the horizontal and vertical lines of sight:
^
|
<-#->
|
v
Altogether forming this pattern:
^^^->
|||->
<-#->
<-|||
<-vvv
Or, following concentric circles:
First pass
\ | /
812
-7#3-
654
/ | \
Next pass
.8.1.
7...2
..#..
6...3
.5.4.
Yikes. This feels overly complicated.
But I've got to try building it!
A visual depiction of the algorithm I plan to build
This demonstrates how the algorithm I plan to build should work:
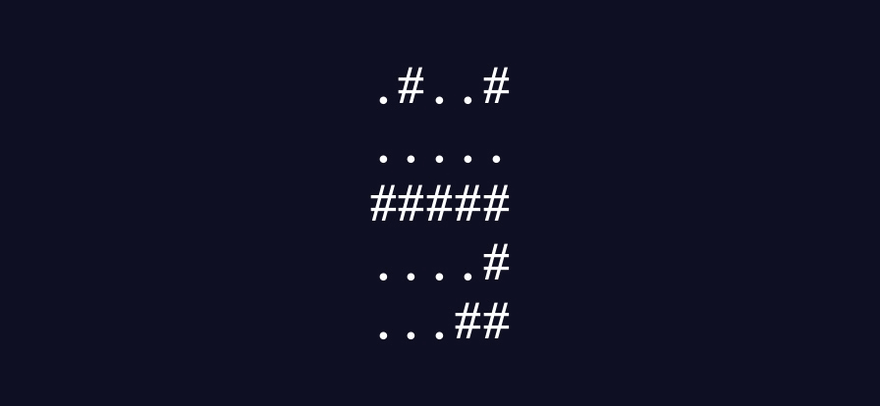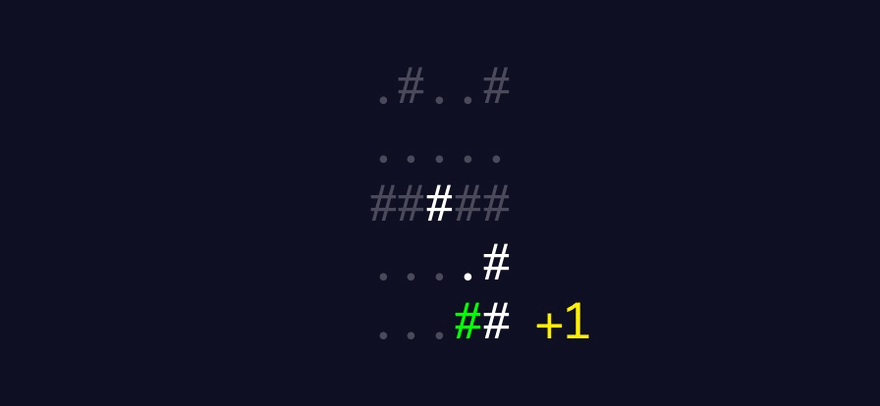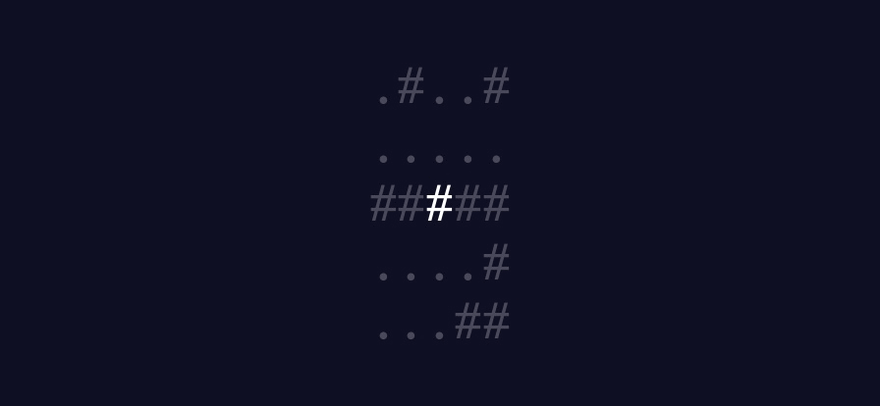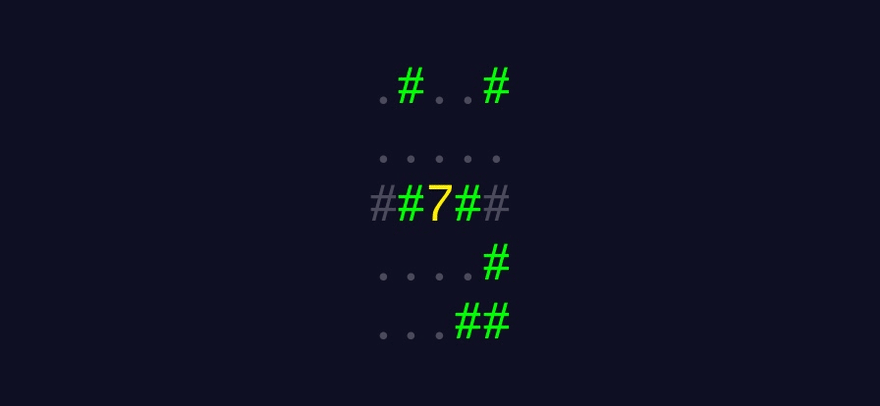
A written summary of how the algorithm should work
For each value in the region map that contains an asteroid
Perform two rounds: one starting from each immediate diagonal coordinate, and another from each horizontally- and vertically-adjacent coordinate
Round 1
For each of the four immediately diagonal coordinates
Visit every cell in that quadrant bordered by the x- and y-axes
Track the tally of asteroids spotted, starting at 0
Track a unique set of values representing coordinates of each visited cell
From each initial cell
Track how many asteroids were spotted via a list of boolean values
Do as long as the cell exists in the map region
As long as the cell hasn't been visited yet
If it is an asteroid, add True to the list of spotted asteroids
Else, add False to the list
Add it to the list of visited cells
Move a distance equal to the relative distance between the originating coordinate and the initial cell's coordinates
If there is at least one True value in the list of spotted asteroids, increment the tally by 1
Return the tally
Return the sum of all four tallies
Round 2
For each of the four horizontally- and vertically-adjacent coordinates
Track the tally of asteroids spotted, starting at 0
Do as long as the cell exists in the map region
If the cell's value is an asteroid
Increment the tally by 1
Break
Else, move one step in the current direction (up, right, down or left)
Return the tally
Return the sum of all four tallies
Return the sum of each sum of tallies
Return the largest sum from the new list of summed tallies
Woah. That worked! I'm shocked!
- I ran it on each example
- Each time it generated the correct answer
- I ran it on my puzzle input
- And it, too, generated the correct answer!
Part 2
- Yikes! Order matters now.
- Throwing in the towel
Yikes! Order matters now.
- We're still counting...
- But from a specific angle...
- In a specific direction...
- So the order of asteroid detection is important
Throwing in the towel
I can't think of an algorithmic way to re-create a pathfinding algorithm akin to the abstract laser rotating in this puzzle.
So, sadly, Part 2 will go unsolved.
Celebrating my accomplishments
- I solved Part 1! I really didn't think I would.
- I made a cool GIF that accurately visualized my peculiar algorithm
Bummer:
- No simulator...mostly because it didn't seem worth it
- No correct answer for Part 2...though I'm content with solving Part 1
Today's puzzle was a wonderful twist on the recurring 'find adjacent things' theme.
And I'm so delighted I solved Part 1.



Top comments (0)