Advent of Code 2021 Day 9
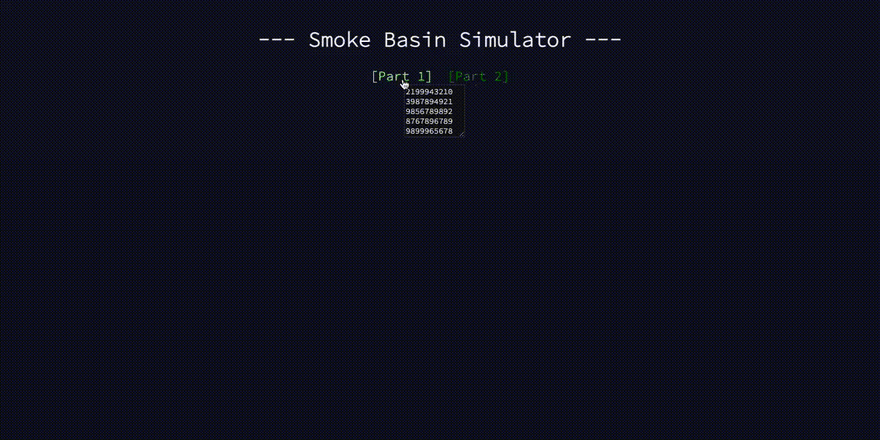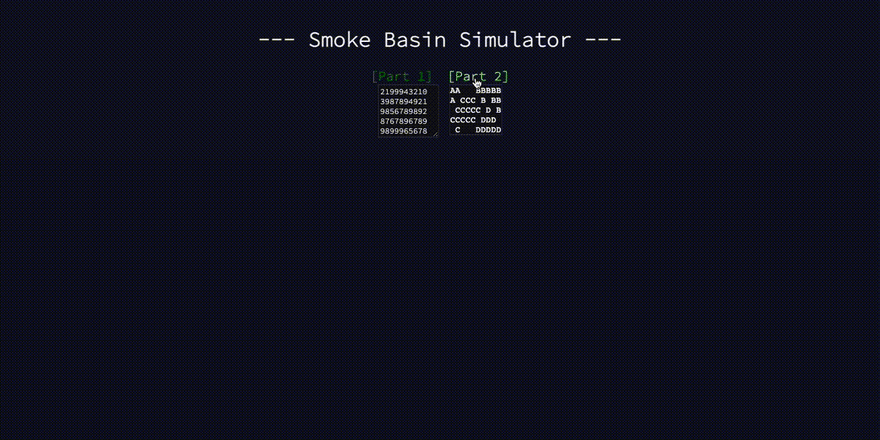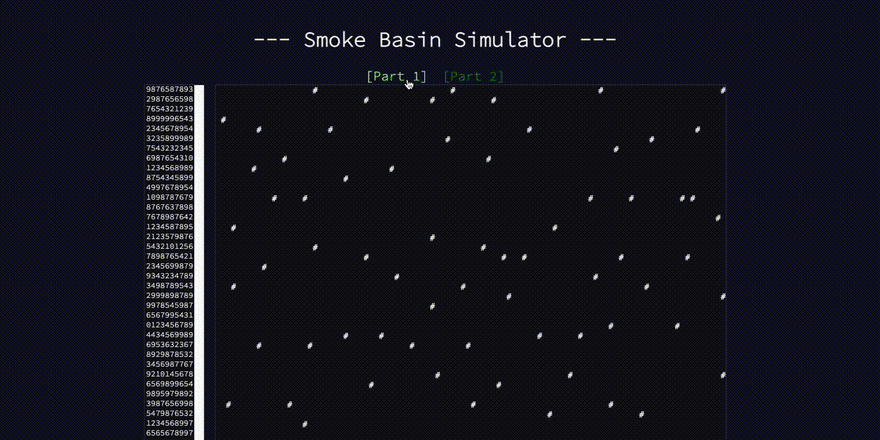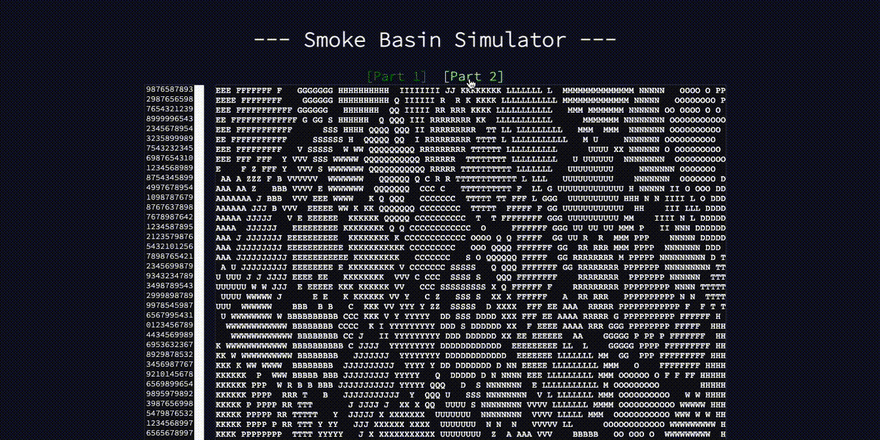
Try the simulator
The task at hand
Solve for X where
X = a combination of individual counts
- Sum of risk levels of each low point
- Product of the size of the three largest basins
Input is
- A multi-line string
It represents
- A 100x100 square area
- Each location is a number between
0-9 - Each number represents an altitude
Part 1: Rounds 1 and 2
I solved this part of the challenge on the day it was released.
In 50 lines of code, my original algorithm looked something like this:
Setup:
Split the file's contents into an array of strings
Split each string into an array of characters
Convert each character into a number 0-9
Create an array to collect low points
Sub-routine to record a low point:
Add the current number to the array of low points, only if:
The minimum number among a list of numbers...
...is equal to the number at the current location...
...and the number in the last location...
...of the sorted and reversed list of numbers...
...is the number at the current location
For each row in the grid
For each cell in the row
Through a series of nested if..else if..else clauses...
...call the sub-routine, passing in the appropriate amount of arguments, each referencing the correct adjacent cell values
For each value in the collection of low points
Update the value to itself plus one
For each value in the incremented collection of low points
Add the value to an accumulating sum of all previous values
Return the final sum
Round 2: Now only 10 lines of code!
Same setup: process input file into a 2D array of numbers
Set risk level to 0
For each row in the grid
For each cell in the row
If the value in the cell is less than...
...the minimum number in a list of 2-4 numbers...
...resulting from a starting array of four relative coordinates (up one, left one, right one, down one)...
...updated to contain the values in each of the cells referenced by those relative coordinates...
...filtered to remove undefined values attained by references to cells that are out of boundary
Increment risk level by the current cell's value plus one
Return risk level
Here's a visual description
Feeling invigorated after refactoring Part 1's code
- I put into practice a slew of new coding tricks I learned from studying other solvers' code in prior challenges
- I resolved a silly mistake in my code that failed to omit cell values that were less than their adjacent cells' values
- I felt proud of the conciseness and eloquence of my code, especially as compared to Round 1
Part 2: Round 1
When it was originally released, I didn't even attempt to solve part 2.
That's because I was unable to understand what was happening in the example diagrams.
This time around - with careful analysis, and perhaps an improved eye for interpreting puzzle instructions - I understood how the size of each basin was determined.
Two ways to solve
- Use
Findin my browser with the query9and my eyes to identify the largest basins and tally the sizes manually
- Write an algorithm that tallies each basin size after processing the entire grid area
Obviously, I felt motivated to solve it via #2.
Defining what the algorithm should return
21 AA
39 A
Given the input on the left, the algorithm should find a basin of size 3
219 AA
399 A
996 B
Given the input above, the algorithm should two basins: one of size 3, another of size 1
89876995 A BBB C
93987896 D BBB C
54598939 DDD B E
95999123 D EEE
89891019 F G EEE
Given the input above, the algorithm should seven basins with sizes: 1,7,2,5,7,1,1
9299999 A
9193939 A A A
9012349 AAAAA
9101999 AAA
9912329 AAAA
9999939 A
Given the input above, the algorithm should find a basin of size 17
And, of course, the example provided:
2199943210 AA BBBBB
3987894921 A CCC B BB
9856789892 CCCCC D B
8767896789 CCCCC DDD
9899965678 C DDDDD
Given the input above, the algorithm should four basins with sizes: 3,9,9,14
Describing how this algorithm should work
Create a unique set to track visited locations
Create an empty list to track basin sizes
For each row in the grid
For each cell in the row
If the cell's value is not 9, and its coordinates are not in the list of traversed cells:
* For each of 2-4 cells above, left, right and below it:
If the cell's value is 9:
Return the locations visited along the way to this cell
Else if the cell's value is 1 higher or lower than the source cell's value:
Continue at * with the current list of visited locations
Add to the list of basins:
The size of the unique set of visited locations in the basin that this cell resides
For each size in basins
Sort the list of basins from largest to smallest
Extract the largest three values
Return the product of all three values
Delight, then disappointment
- Running my algorithm on each of the samples above produces the correct output: it found each basin and determined the size correctly
- Sadly, when I ran my algorithm on my input, the answer it generated was too low
- To diagnose, I searched for a large-looking basin in my output. I found one at the bottom. I counted the values. I ran my algorithm. I found a problem.

UPDATED: Then extreme delight!
I solved it later the same day! See my revised notes below to learn how I stumbled upon - and resolved - my algorithm's error.
A summary of my journey through this challenge
- I solved Part 1 a while ago
- At that time, I didn't understand Part 2 enough to even attempt it
- Now, I solved Part 1 with an algorithm 1/5 the original's size!
- I actually understand what's happening in Part 2
- I wrote an algorithm that generates the correct answer on several small example data sets
- I discovered an example basin that my algorithm doesn't properly compute, in case I ever want to come back and meticulously debug it
My reflection from before solving Part 2:
It's a bummer that I couldn't solve Part 2.
I'm definitely proud of how much progress and practice this challenge offered me.
Now, it's time to move on.
Part 2: Round 2
- I came back later the same day to investigate how my algorithm processed that basin
- I discovered a new truth about the numbers in the grid: they may not always change by 1 from cell to cell

- I removed parts of my code that were overly conditional
- I generated the correct answer for Part 2!
- Bonus: I made another simulator to show the low points and basins for any valid grid
My reflection from after solving Part 2:
Just kidding!
It turns out, I couldn't let this puzzle go unsolved.
Luckily, with a simple logging statement, I could see which locations my algorithm started from.
Upon reviewing the first unexpected starting location, I noticed it was a difference of 2 from each of its adjacent cells.
I assumed there was only ever a difference of 1.
I removed that condition from my code.
Viola! My algorithm now calculated the correct - larger - sizes of each basin...and thus determined the correct product of the three largest basins
What a huge relief, fantastic sense of closure, and an incredibly rewarding personal achievement!
Bonus for code golf fans: my final code for both solutions is only 40 lines.
Next!




Top comments (0)