865. Smallest Subtree with all the Deepest Nodes

#php #leetcode #algorithms #programming

Difficulty: Medium

Topics: Hash Table, Tree, Depth-First Search, Breadth-First Search, Binary Tree, Weekly Contest 92

Given the root of a binary tree, the depth of each node is the shortest distance to the root.

Return the smallest subtree such that it contains all the deepest nodes in the original tree.

A node is called the deepest if it has the largest depth possible among any node in the entire tree.

The subtree of a node is a tree consisting of that node, plus the set of all descendants of that node.

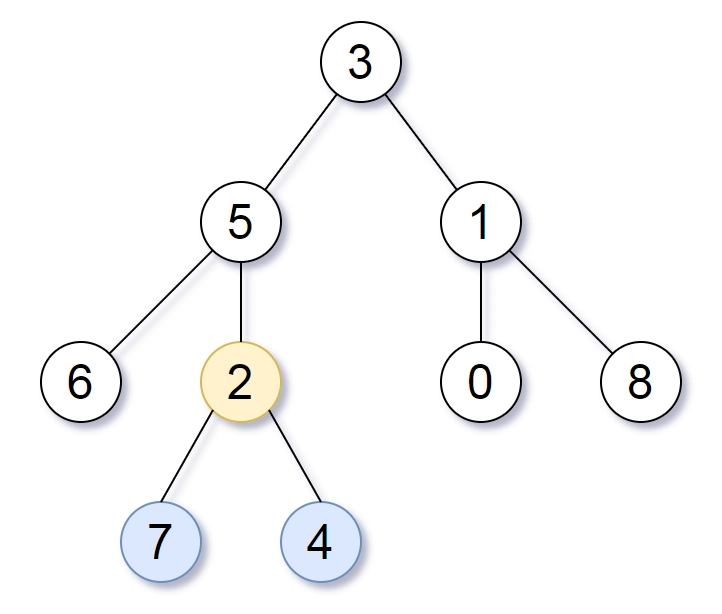
Example 1:

Input: root = [3,5,1,6,2,0,8,null,null,7,4]
Output: [2,7,4]
Explanation: We return the node with value 2, colored in yellow in the diagram.
- The nodes coloured in blue are the deepest nodes of the tree.
- Notice that nodes 5, 3 and 2 contain the deepest nodes in the tree but node 2 is the smallest subtree among them, so we return it.

Example 2:

Input: root = [1]
Output: [1]
Explanation: The root is the deepest node in the tree.

Example 3:

Input: root = [0,1,3,null,2]
Output: [2]
Explanation: The deepest node in the tree is 2, the valid subtrees are the subtrees of nodes 2, 1 and 0 but the subtree of node 2 is the smallest.

Constraints:

The number of nodes in the tree will be in the range [1, 500].
0 <= Node.val <= 500
The values of the nodes in the tree are unique.

Note: This question is the same as 1123. Lowest Common Ancestor of Deepest Leaves

Solution:

We eed to find the smallest subtree containing all deepest nodes. Essentially, we need to find the lowest common ancestor of all deepest leaves.

Approach:

I'll use a recursive approach where each node returns:

The depth of the deepest node in its subtree
The node that is the LCA of deepest nodes in its subtree

Key Insight:

For each node, compare the depths of its left and right subtrees
If both subtrees have the same maximum depth, then this node is the LCA for deepest nodes in both subtrees
Otherwise, the LCA is from the subtree with greater depth

Let's implement this solution in PHP: 0865. Smallest Subtree with all the Deepest Nodes

<?php
/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     public $val = null;
 *     public $left = null;
 *     public $right = null;
 *     function __construct($val = 0, $left = null, $right = null) {
 *         $this->val = $val;
 *         $this->left = $left;
 *         $this->right = $right;
 *     }
 * }
 */
class Solution {

    /**
     * @param TreeNode $root
     * @return TreeNode|null
     */
    function subtreeWithAllDeepest(TreeNode $root): ?TreeNode
    {
       ...
       ...
       ...
       /**
        * go to ./solution.php
        */
    }

    /**
     * @param $root
     * @param $p
     * @param $q
     * @return mixed
     */
    private function findLCA($root, $p, $q): mixed
    {
       ...
       ...
       ...
       /**
        * go to ./solution.php
        */
    }
}

/**
 * @param array $arr
 * @return TreeNode|null
 */
function buildTree(array $arr): ?TreeNode {
    if (empty($arr)) return null;

    $root = new TreeNode(array_shift($arr));
    $queue = new SplQueue();
    $queue->enqueue($root);

    while (!$queue->isEmpty() && count($arr) > 0) {
        $node = $queue->dequeue();

        $leftVal = array_shift($arr);
        if ($leftVal !== null) {
            $node->left = new TreeNode($leftVal);
            $queue->enqueue($node->left);
        }

        if (count($arr) === 0) break;

        $rightVal = array_shift($arr);
        if ($rightVal !== null) {
            $node->right = new TreeNode($rightVal);
            $queue->enqueue($node->right);
        }
    }

    return $root;
}

/**
 * @param TreeNode|null $root
 * @return array
 */
function printSubtree(?TreeNode $root): array {
    if (!$root) return [];

    $res = [];
    $queue = new SplQueue();
    $queue->enqueue($root);

    while (!$queue->isEmpty()) {
        $node = $queue->dequeue();
        $res[] = $node->val;

        if ($node->left) $queue->enqueue($node->left);
        if ($node->right) $queue->enqueue($node->right);
    }
    return $res;
}


// Test cases
$solution = new Solution();

/**
 * Test Case 1
 * Input: [3,5,1,6,2,0,8,null,null,7,4]
 * Output: [2,7,4]
 */
$root1 = buildTree([3,5,1,6,2,0,8,null,null,7,4]);
$result1 = $solution->subtreeWithAllDeepest($root1);
print_r(printSubtree($result1));
// Expected Output: [2, 7, 4]


/**
 * Test Case 2
 * Input: [1]
 * Output: [1]
 */
$root2 = buildTree([1]);
$result2 = $solution->subtreeWithAllDeepest($root2);
print_r(printSubtree($result2));
// Expected Output: [1]


/**
 * Test Case 3
 * Input: [0,1,3,null,2]
 * Output: [2]
 */
$root3 = buildTree([0,1,3,null,2]);
$result3 = $solution->subtreeWithAllDeepest($root3);
print_r(printSubtree($result3));
// Expected Output: [2]


/**
 * Test Case 4 (deepest nodes on both sides)
 * Input: [1,2,3,4,5]
 * Output: [1]
 */
$root4 = buildTree([1,2,3,4,5]);
$result4 = $solution->subtreeWithAllDeepest($root4);
print_r(printSubtree($result4));
// Expected Output: [1]


/**
 * Test Case 5 (left-heavy tree)
 * Input: [1,2,null,3,null,4]
 * Output: [4]
 */
$root5 = buildTree([1,2,null,3,null,4]);
$result5 = $solution->subtreeWithAllDeepest($root5);
print_r(printSubtree($result5));
// Expected Output: [4]
?>

Explanation:

The recursive solution is more elegant and efficient. Here's how it works:

For each node, recursively get results from left and right children
Each result contains:
- The LCA of deepest nodes in that subtree
- The maximum depth in that subtree
Compare depths:
- If equal: current node becomes LCA (deepest nodes are in both subtrees)
- If left deeper: left's LCA becomes current LCA
- If right deeper: right's LCA becomes current LCA
Return result with depth incremented by 1

The base case is when node is null (depth 0, LCA null).

Complexity

Time Complexity: O(N) where N is the number of nodes

The recursive approach visits each node exactly once
The BFS approach also visits each node once, plus LCA calculations

Space Complexity: O(H) where H is the height of the tree

For recursion, it's the recursion stack depth
For BFS, it's O(N) in worst case for storing deepest leaves

Contact Links

If you found this series helpful, please consider giving the repository a star on GitHub or sharing the post on your favorite social networks 😍. Your support would mean a lot to me!