Daily Challenge #112 - Functions of Integers on the Cartesian Plane

Consider integer coordinates x, y in the Cartesian plane and three functions f, g, h defined by:

f: 1 <= x <= n, 1 <= y <= n --> f(x, y) = min(x, y)
g: 1 <= x <= n, 1 <= y <= n --> g(x, y) = max(x, y)
h: 1 <= x <= n, 1 <= y <= n --> h(x, y) = x + y

where n is a given integer (n >= 1, guaranteed) and x, y are integers.

In the table below you can see the value of f(n) where n = 6.

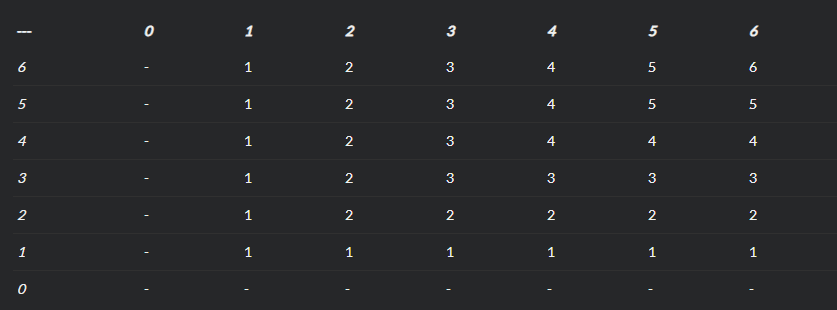
The challenge is to calculate the sum of f(x, y), g(x, y), and h(x, y) for all integers x and y such that (1 <= x <= n, 1 <= y <= n)

The function sumin (sum of f) will take n as a parameter and return the sum of min(x, y) in the domain 1 <= x <= n, 1 <= y <= n. The function sumax (sum of g) will take n as a parameter and return the sum of max(x, y) in the same domain. The function sumsum (sum of h) will take n as a parameter and return the sum of x + y in the same domain.

sumin(6) --> 91
sumin(45) --> 31395
sumin(999) --> 332833500
sumin(5000) --> 41679167500

sumax(6) --> 161
sumax(45) --> 61755
sumax(999) --> 665167500
sumax(5000) --> 83345832500

sumsum(6) --> 252
sumsum(45) --> 93150
sumsum(999) --> 998001000
sumsum(5000) --> 125025000000

Hints:

• Try to avoid nested loops.
• Note that h = f + g

Good luck!

---

This challenge comes from g964 on CodeWars. Thank you to CodeWars, who has licensed redistribution of this challenge under the 2-Clause BSD License!

Want to propose a challenge idea for a future post? Email [e-mail] with your suggestions!

Comments

[Craig McIlwrath]

No loops required!

summin n = n * (n + 1) * (2*n + 1) `div` 6

summax n = n*n*n - summin (n - 1)

sumsum n = n*n*n + n*n

I'll put my thought process here because those equations look pretty arbitrary.

From that example grid of values of f, you can see the sum is 1*(n² - (n-1)²⁾ + 2 * ((n-1)² - (n-2)²⁾ + ... when you expand that out you get the sum of the first n squares. Which is the formula in summin (that Google lead me to).

For g, you can produce a chart of its value by taking an nxn square of n's, then subtracting the area of each square smaller than that. e.g. n*n*n - (n - 1)² - (n - 2)² -... which is the same as n*n*n - summin (n-1)

sumsum could be just the sum of the other two functions, but that's too simple. if you math it out, you get n*n*n + n*n. Much better.

[Vitaliy Kononenko]

Elegant challenge. We can notice that f and g are complementary to each other. We can draw the grid for f and g and notice, that sum of these grids is equal to sum of the gride of size n*n with (n+1) value is each cell. So the sum of f and g is equal to n*n*(n+1). The sum h is also equal to f + g.

fun fghSum(n: Long) = n * n * (n + 1) * 2